П.2.7.3. Распределение частот

Существует множество отношений между переменными, при которых каждое значение зависимой переменной, соответствующее значению независимой переменной, представляет собой число событий, приходящихся на данное значение независимой переменной, т. е. ее частоту. Такие отношения можно описать функцией распределения частот, или просто распределением, например, дождевых червей по длине тела в популяции.

Если независимая переменная может принимать любые значения в пределах данного ряда, то распределение частот можно представить в виде обычного графика, как это описано выше. Такие графики называются кривыми распределения и в зависимости от рода данных могут иметь одну из форм, описанных ниже. Если данные представляют собой численность организмов в пределах определенного интервала, как показано на рис. П.2.10, А, то распределение называется непрерывным, а все пространство под кривой составляет общую частоту событий.

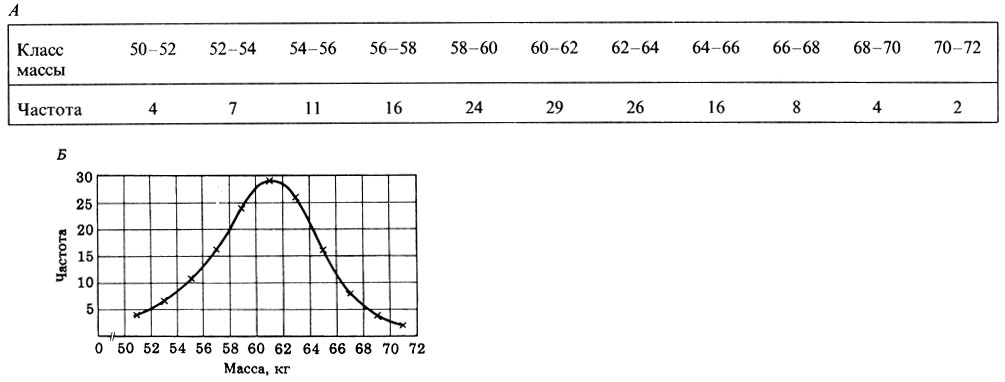
Рис. П.2.10. А. Представленная в виде таблицы численность 18-летних мужчин в каждом классе массы по 2 кг. Б. Графическое изображение данных из табл. А. дает кривую нормального распределения

1. Кривая нормального распределения. В этом случае распределение частот симметрично относительно центрального значения, а рассматриваемые переменные относятся к физическим параметрам, таким, как рост или масса биологического объекта. Этот тип распределения показан на рис. П.2.10.

2. Положительный уклон. Кривая распределения в этом случае несимметрична. Наибольшие частоты независимой переменной приходятся на ее более низкие значения, а по направлению к более высоким значениям кривая начинает "хвостить" (рис. П.2.11, А). В качестве примера такого распределения можно привести распределение числа детей, приходящихся на одну семью, размеров кладки у птиц, плотности фитопланктона с увеличением глубины.

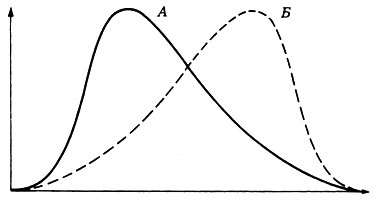
Рис. П.2.11. А. Распределение с положительным уклоном. Б. Распределение с отрицательным уклоном

3. Отрицательный уклон. В этом случае наибольшие частоты независимой переменной приходятся на ее более высокие значения, а по направлению к более низким значениям кривая начинает "хвостить" (рис. П.2.11, Б). Эта форма распределения встречается реже, чем предыдущая; она характерна для распределения некоторых форм смещения. Например, распределение оптимальных температур ферментативных реакций и выработка стимулирующих гормонов щитовидной железы в ответ на действие тироксина.

4. Бимодальное распределение. В этом случае наблюдаются два максимума (или два пика), что обычно указывает на присутствие двух популяций, для каждой из которых характерно неполное нормальное распределение.

5. Совокупное распределение частот. Данные, представленные на рис. П.2.10, можно также представить, как на рис. П.2.12. Здесь показано совокупное число организмов, находящихся ниже определенного произвольно выбранного класса границ. Если эти данные изобразить графически, то получится кривая совокупного распределения частот.

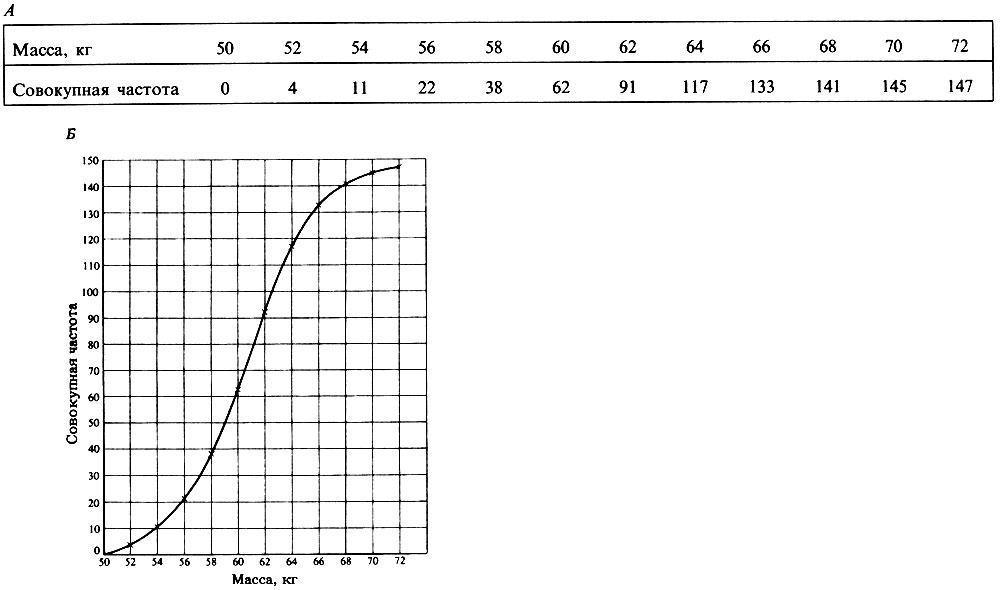
Рис. П.2.12. Таблица (А ) и график (Б), построенные на основе рис. П.2.10, А, представляющие совокупную частоту распределения массы среди 18-летних мужчин

Если независимая переменная принимает дискретные значения, например целые числа 3 и 5 (как число лепестков у двудольных), или ею представлены физические признаки, такие, например, как группы крови, которые характеризуются дискретными значениями, то распределение не будет непрерывным. В этом случае нельзя начертить непрерывную кривую, поэтому используются другие, описанные ниже формы графического изображения данных.

1. Диаграмма в виде вертикальных столбцов. Она показывает частоту, с которой определенные признаки встречаются внутри популяции. Например, частота групп крови у человека (см. рис. П.2.13, А).

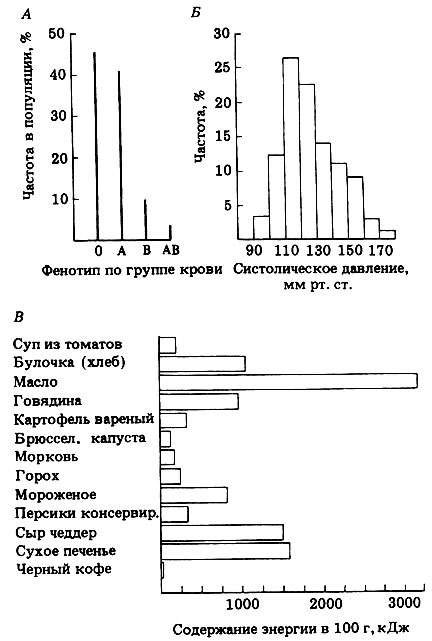
Рис. П.2.13. Способы представления данных. А. Диаграмма с вертикальным расположением столбцов, показывающая фенотипы по группам крови в популяции. Б. Гистограмма, показывающая частоту различного систолического кровяного давления у женщин в возрасте от 30 до 39 лет. В. Диаграмма с горизонтальным расположением столбцов, показывающая содержание энергии в пище (при трехразовом питании)

2. Гистограмма. Она строится на непрерывных значениях независимой переменной, сгруппированных в классы равной ширины. Когда классы равной ширины выбраны, например 0-5, 5-10, 10-15 и т. д., границы интервалов обычно проходят по числам меньшим, чем указанные целые значения, т. е. 0-4,99; 5-9,99; 10-14,99 и т. д. В форме гистограммы удобно представлять данные, характеризующие наибольшие выборки. Внешне гистограммы похожи на диаграммы в виде вертикальных столбцов (рис. П.2.13, Б).

3. Диаграмма в виде горизонтальных столбцов. Это видоизмененная форма гистограммы. Она обычно используется для того, чтобы показать отношения между непрерывной зависимой переменной, например содержанием энергии, и нечисловой независимой переменной, например различными видами пищи (рис. П.2.13, В). Видоизмененная форма горизонтальной диаграммы используется для представления экологических данных; она называется диаграммой присутствия-отсутствия (см. рис. 13.21).

4. Кайт-диаграмма. Это особый тип горизонтальной диаграммы, который дает предельно ясное наглядное изображение изменения частот неисчисляемых переменных непрерывно распределенных в пределах определенной площади. Кайт-диаграмма строится путем нанесения частот каждой переменной в виде параллельных отрезков, перпендикулярных оси х (см. рис. П.2.14, А).

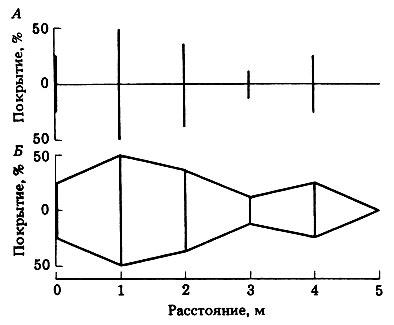
Рис. П.2.14. Способы построения кайт-диаграммы (от англ. kite-бумажный змей)

После того как все частоты нанесены вдоль оси х, соседние концы отрезков соединяются прямыми линиями как при построении линейного графика (см. рис. П.2.14, Б). Заключенную внутрь фигуры площадь обычно заштриховывают, чтобы получить более наглядное изображение. О применении кайт-диаграмм распределения рассказано в разд. 13.4.3.

Каждый из описанных выше способов представления данных используется при решении различных биологических задач. Все перечисленные способы изложены в различных главах этой книги. Каждый метод имеет свои достоинства. При выборе того или иного метода следует руководствоваться тем, как можно наиболее точно и рационально продемонстрировать связи и характер отношений между переменными.