2.3. Пассивный транспорт растворенных веществ

Трансмембранный градиент концентраций молекул растворенного вещества вызывает перемещение этого вещества по направлению его градиента.

В простейшем случае скорость потока молекул растворенного вещества по направлению его концентрационного градиента (поток J) может быть описана законом простой диффузии (закон Фика), который выражается уравнением

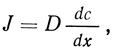
где D - коэффициент простой диффузии, a dc/dx - концентрационный градиент или химический градиент. D можно заменить выражением ωRT (ω - подвижность, a RT - кинетическая энергия системы).

На движение ионов влияет также электрический градиент. В этом случае скорость потока растворенного вещества описывается уравнением Нернста - Планка

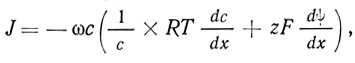
где z - число электрических зарядов на проникающей молекуле, F - число Фарадея (96 500 Кл/моль), dφ/dx - трансмембранный градиент заряда. Выражение в скобках представляет собой комбинацию химического и электрического градиентов и обозначается как электрохимический градиент.

Эти два уравнения полностью описывают процесс простого пассивного передвижения растворенного вещества через мембраны.

Изучение скорости пассивного движения различных веществ через клеточные мембраны дает важную информацию о физической и химической природе этих барьеров. Количественный анализ явления проницаемости осложняется тем, что через мембрану движутся одновременно молекулы и растворителя и растворенного вещества. Однако были предложены методы, позволяющие обойти указанные затруднения и облегчающие количественную оценку проницаемости различных природных и искусственных мембран. Так, например, один из предложенных методов позволяет прослеживать изменения объема эритроцитов, обусловленные возникновением трансмембранного градиента концентрации какого-либо проникающего через мембрану неэлектролита. График зависимости изменений объема от времени может быть экстраполирован к нулевому моменту времени, что позволяет получить начальную скорость транспорта. Дальнейшие экстраполяции можно провести в экспериментах с растворами других веществ (например, глицерином, сахарозой, мочевиной и формамидом), варьируя в каждом случае градиенты концентраций. По данным таких экспериментов вычисляют параметры проницаемости, выражающиеся в радиусах гипотетических пор, через которые могут свободно пройти молекулы исследуемых веществ. Вот некоторые радиусы таких пор (нм):

 эритроцит человека       - 0,42, 
 мышечное волокно лягушки - 0,40,
 аксон кальмара           - 0,42, 
 почка саламандры         - 0,56.

Расчет параметров проницаемости включает ряд допущений относительно применимости различных физических законов для описания движения молекул через мембраны. Несмотря на это, получаемые величины радиусов пор дают хорошую основу для сравнения проницаемости различных клеточных мембран по отношению к воде и другим малым незаряженным молекулам.

Природа и локализация таких пор неизвестны, и поэтому поры и радиусы пор следует считать чисто гипотетическими понятиями, а величины радиусов можно использовать только как основу для сравнительного изучения различных мембран.

Изучая скорости проникновения различных органических веществ-неэлектролитов в клетки растений и животных, ученые уже очень давно пришли к заключению (Овертон, 1899), что растворимость веществ в маслах или неполярных растворителях является важным фактором, определяющим скорость такого проникновения. Исследования, проведенные на клетках Chara ceratophilla, демонстрируют близкую к линейной зависимость транспорта через клеточные мембраны от коэффициента распределения проникающего вещества между водой и маслом. Размер молекул также влияет на их способность проникать через мембраны, причем это влияние только частично отражено в соответствующем изменении коэффициента распределения вещества между водой и маслом. Так, анализ данных по способности малых молекул проникать в клетки Chara показывает, что приближение характера этой зависимости к линейному наблюдается только в том случае, если учитывать такой фактор, как размер молекул, иными словами - изучать зависимость Р×М¹/² от коэффициента распределения (рис. 23).

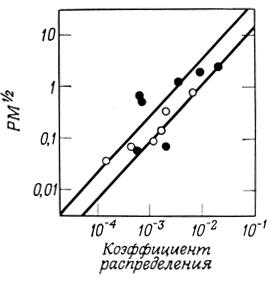
Рис. 23. Зависимость скорости проникновения через мембрану некоторых органических неэлектролитов от их молекулярного веса и коэффициента распределения между водой и маслом. Светлые кружки - мочевина; черные кружки - амиды (RCONH₂); Р - проницаемость; М - молекулярный вес

Скорость проникновения некоторых неэлектролитов через искусственные фосфолипидные мембраны (липосомы), а также через мембраны изолированных клеток, таких, как эритроциты, опухолевые клетки и бактерии, сильно зависит от температуры. Подобная зависимость рассматривается как свидетельство того, что молекулы проникающего вещества проходят сквозь гидрофобную область мембраны, состоящую из углеводородных остатков липидных молекул. Эта точка зрения подтверждается в опытах, в которых меняли вязкость гидрофобной области липидного слоя посредством изменения соотношения ненасыщенных углеводородных цепей и холестерина в липидной фазе.

Энергию активации (Е) процесса проникновения веществ через мембрану можно вычислить из зависимости скорости проникновения от величины, обратной температуре (рис. 24). Например, значения энергии активации, полученные для этиленгликоля, глицерина и эритрита (соответственно 60, 77 и 87 кДж/моль; 1 кДж = 4,2 ккал), близки к значениям энергии их дегидратации. Таким образом, весьма вероятно, что дегидратация молекул этих соединений является предварительным условием их входа в липидный слой мембраны. Дальнейшее движение молекул контролируется, по-видимому, вязкостью углеводородной части мембраны.

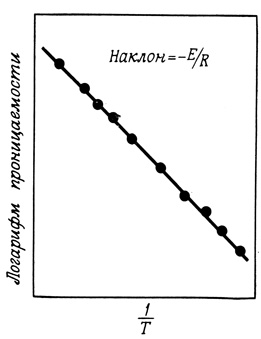
Рис. 24. Зависимость проницаемости от температуры

Энергетический барьер при переносе специфических молекул через мембрану может быть описан в терминах профиля потенциальной энергии, используемых для иллюстрации теории абсолютных скоростей (рис. 25). Из этой теории следует, что перенос молекул растворенного вещества через мембрану осуществляется скачками из одного равновесного положения в другое. Наибольший энергетический барьер для молекул неэлектролита, движущегося через мембрану по направлению своего химического градиента, возникает на стадии входа в мембрану. Именно поэтому, вероятно, прежде чем пройти через полярный барьер заряженных групп фосфолипида, молекуле необходимо освободиться от гидратной оболочки.

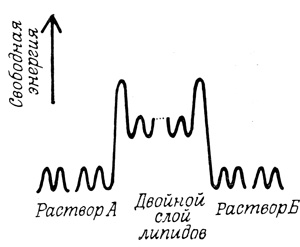
Рис. 25. Профиль потенциальной энергии при переносе молекул растворенного вещества через мембрану, образованную двойным слоем липидов