
Математическая модель гетерогенной каталитической системы с промежуточным субстратом
Рассмотрим двухстадийную каталитическую реакцию, протекающую в пластине (мембране) с равномерно распределенным по ее объему ферментом, в предположении, что концентрации субстратов в растворе у поверхности мембраны поддерживаются постоянными. Пусть первоначально мембрана с иммобилизованным ферментом насыщена вторым субстратом в форме S2', равновесна распределенным между раствором и твердой фазой. Затем в систему вводится избыток S1, который переводит S2' в растворе в форму S2; это же превращение второго субстрата происходит по мере диффузии S1 внутрь пластины. Для простоты предположим, что равновесное распределение второго субстрата между фазами не нарушается при изменении его состояния, т. е. коэффициенты распределения S2 и S2' одинаковы. Концентрация протонов в процессе реакции не изменяется вследствие высокой концентрации буферного раствора.
В соответствии с двухстадийной схемой реакции (2.59) в мембране образуются две зоны реакции (рис. 22). В первой зоне установится избыточная концентрация S1, и второй субстрат будет полностью переведен в форму S2. Образующаяся на второй стадии реакции форма S2' в присутствии S1 снова мгновенно превращается в S2. Во второй зоне второй субстрат находится в первоначальной форме S2'. В стационарном режиме диффузионные потоки S2' слева и S2' справа на границе двух зон компенсируют друг друга. Образующийся на границе субстрат S2 диффундирует во вторую зону мембраны, где расходуется по второй стадии реакции.
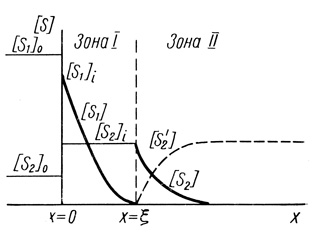
Рис. 22. Схема профиля концентраций в системе двух последовательных реакций
Выражение для скорости ферментативной реакции имеет вид
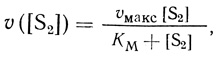 (2.60)
(2.60)где υ - локальная скорость реакции, определяемая далее как скорость восстановления протонов; υмакс - максимальная скорость реакции, зависящая от концентрации фермента; [S2] - локальная концентрация второго субстрата; КМ - константа Михаэлиса иммобилизованного фермента. В первой зоне скорость реакции постоянна по толщине пластины и равна υ([S2]i), где [S2]i - концентрация второго субстрата, равновесная с концентрацией во внешнем растворе [S2]0.
При сделанных предположениях краевая задача формулируется следующим образом:
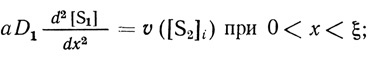 (2.61)
(2.61) (2.62)
(2.62)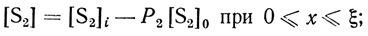 (2.63)
(2.63)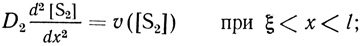 (2.64)
(2.64) (2.65)
(2.65)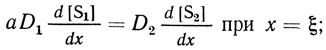 (2.66)
(2.66) (2.67)
(2.67)где [S1] - локальная концентрация S1 в мембране; [S1]0 и [S2]0 - концентрации субстратов в растворе; D1 и D2 - коэффициенты диффузии; Р1 и Р2 - коэффициенты распределения субстратов соответственно; х - расстояние от поверхности мембраны; ξ - координата границы двух зон; l - координата плоскости симметрии мембраны, либо толщина мембраны, если с раствором контактирует лишь одна сторона ее поверхности; локальная концентрация S2' удовлетворяет равенству [S2'] = [S2]0 - [S2].
Выражение для потока продукта - молекулярного водорода - с учетом стехиометрических коэффициентов выглядит следующим образом:
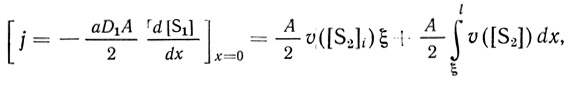 (2.68)
(2.68)где А - площадь поверхности пластины.
Возможен особый случай, когда субстрат S1 диффундирует через всю пластину (ξ = l); процесс переходит в чисто кинетическую область, тогда
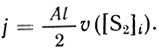 (2.69)
(2.69)Необходимо определить число параметров, полностью описывающих поведение системы. Для этого перейдем к безразмерным переменным η = x/l; θ1 = [S1]/P1[S1]0; θ2 = [S2]/P2[S2]0; ξ* = ξ/l. Система уравнений (2.61)-(2.67) примет вид:
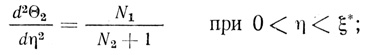 (2.70)
(2.70) (2.71)
(2.71) (2.72)
(2.72)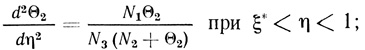 (2.73)
(2.73) (2.74)
(2.74)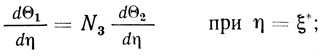 (2.75)
(2.75) (2.76)
(2.76)где
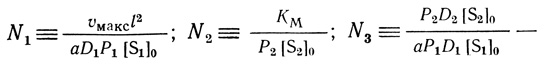
безразмерные комплексы. Вместо уравнения (2.68) имеем
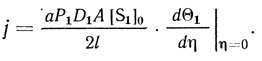 (2.77)
(2.77)Производная dθ1/dη (η = 0) зависит от безразмерных комплексов N1, N2 и N3. Таким образом, поток из пластины определяется этими тремя комплексами N1, N2, N3 и размерным комплексом aP1D1A[S1]0/l. Отсюда следует вывод, что экспериментальное исследование потока продукта из пластины позволяет определить не более четырех параметров системы. Например, если экспериментально исследуют зависимость j от внешних параметров системы [S1]0, [S2]0, l и А, то из этих данных можно рассчитать не более четырех комбинаций внутренних параметров, входящих в выражениях N1, N2 и N3, а именно υмакс и комплексы KМ/P2, aP1D1 и P2D2.
Общее решение задачи. Используем преобразования yj = dθj/dη, где j = 1, 2; тогда d2θj/dη2 = dyj(dyj/dθj) и уравнения (2.70) и (2.72) примут вид:
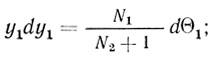 (2.78)
(2.78)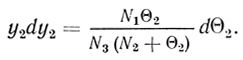 (2.79)
(2.79)Интегрированием (2.78) от η = 0 до η = ξ* было получено
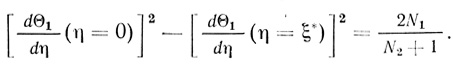 (2.80)
(2.80)Интегрированием (2.79) с учетом (2.76) и (2.72) было найдено
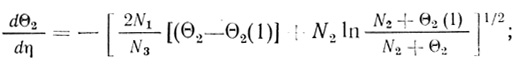 (2.81)
(2.81)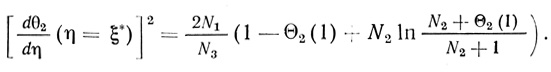 (2.82)
(2.82)Соотношения (2.80), (2.75) и (2.82) позволяют выразить поток продукта через концентрацию θ2.
Чтобы найти θ2(1) и координату границы зон ξ*, интегрировали (2.70) с учетом (2.71) и (2.73), получили
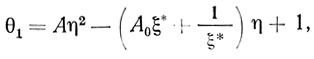 (2.83)
(2.83)где А0 ≡ N1/2(N2 + 1). Из условия (2.75), используя (2.82) и (2.83), запишем
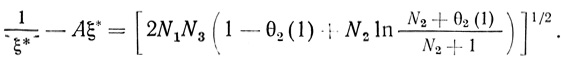 (2.84)
(2.84)Интегрированием (2.81) от η = ξ* до η = 1 с учетом (2.72) найдено
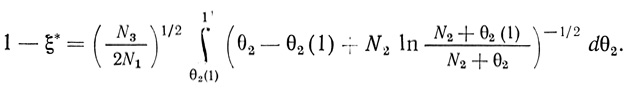 (2.85)
(2.85)Система уравнений (2.84), (2.85) определяет искомые значения ξ* и θ2(1).
Основная трудность при численном решении системы (2.84), (2.85) заключается в вычислении интеграла в правой части уравнения (2.85). При θ2 = θ2(1) подынтегральная функция имеет особенность, однако нетрудно показать, что этот несобственный интеграл сходится. Подстановкой
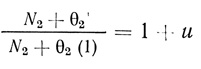
интеграл, входящий в уравнение (2.85), приводится к виду
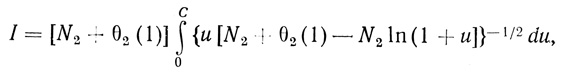
где
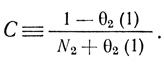
При использовании формулы Тейлора получено
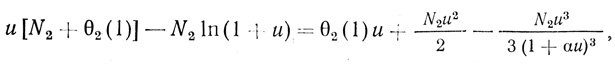
где 0 < а < 1. Отсюда следует
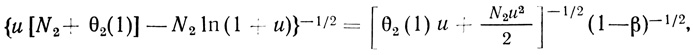
где
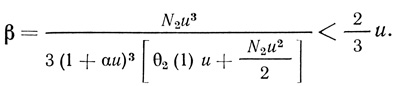
Вторично применяя формулу Тейлора, имеем
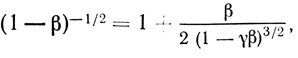
где 0 < y < 1.
Пусть u0 = 10-3, тогда
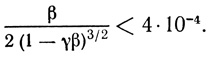
Таким образом, интеграл, входящий в (2.85), можно представить в виде суммы I = I1 +I2, где
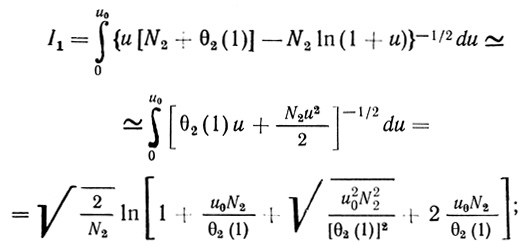 (2.86)
(2.86)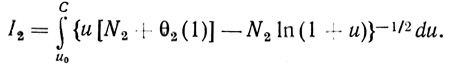 (2.87)
(2.87)При u0 = 10-3 первый интеграл вычисляется по аналитическому выражению (2.86) с точностью до 0,04%. Второй интеграл можно рассчитать с любой точностью стандартными численными методами.
Отметим, что указанный метод вычисления интеграла можно использовать для односубстратной реакции, протекающей по уравнению Михаэлиса-Ментен, в пластине конечной толщины [363-365]. Соответствующая задача приводит к уравнению (2.85), где ξ* = 0.
Асимптотические приближения. Рассмотрим полученное решение в различных асимптотических приближениях.
а) Пластина бесконечно большой толщины. При достаточно больших N1 можно считать, что вдали от поверхности пластины концентрация [S2] убывает до нуля, т. е. вместо граничного условия (2.87) можно использовать условие
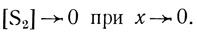 (2.88)
(2.88)Соответствующее данной постановке задачи выражение для потока найдем, положив в формулу (2.82) θ2(1) = 0. В результате получим
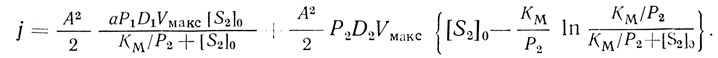 (2.89)
(2.89)При [S1] = 0 формула (2.89) переходит в известное уравнение для односубстратной реакции 354, 357, 358 (см. табл. 21).
б) Ступенчатый фронт реакции. Пусть N3 → 0. Тогда по условию (2.75) профиль концентрации θ2 в окрестности точки ξ* должен быть гораздо более резким, чем профиль θ1. Это означает, что область основного изменения концентрации θ2 будет мала по сравнению с протяженностью первой зоны. В этом случае вклад второго интеграла в правой части (2.68) в суммарное производство продукта будет незначительным.
Упростим соответствующим образом постановку задачи, пренебрегая потоком S1 на границе зон, т. е. поставим вместо условия сопряжения (2.75) условие
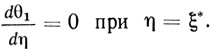 (2.90)
(2.90)Система уравнений для θ2 (2.72), (2.73) и (2.76) вырождается при этом в ступенчатую функцию
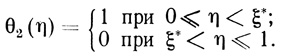 (2.91)
(2.91)Соответственно функция скорости реакции изменяется в точке ξ* ступенчатым образом от υ([S2]i) до 0.
Из уравнений (2.83) и (2.90) найдено
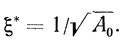 (2.92)
(2.92)Отсюда по формуле (2.68)
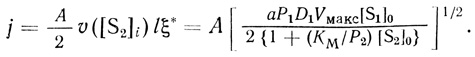 (2.93)
(2.93)Уравнение (2.84) позволяет строго получить достаточные условия применимости ступенчатой модели. Из этого уравнения имеем
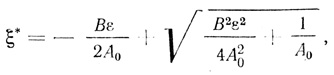
где B ≡ (2N1N3)1/2;
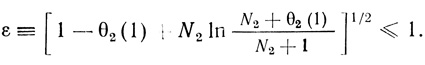 (2.94)
(2.94)Очевидно, что при B2/4A0 << 1 равенство (2.97) переходит в (2.92). Таким образом, достаточным условием применимости ступенчатой модели будет
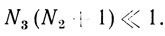 (2.95)
(2.95)|
ПОИСК:
|
© BIOLOGYLIB.RU, 2001-2020
При копировании ссылка обязательна:
http://biologylib.ru/ 'Библиотека по биологии'
При копировании ссылка обязательна:
http://biologylib.ru/ 'Библиотека по биологии'