5. Кинетика действия ферментов в открытых системах. Образование водорода клетками гидрогеназсодержащих микроорганизмов

Ферменты в нативном состоянии действуют как катализаторы химических реакций в открытых системах. Изучение поведения ферментов в открытых системах имеет не только фундаментальное, но и прикладное значение. Развитие экспериментальных и теоретических методов изучения кинетики действия ферментов в этих условиях существенно способствует пониманию многих особенностей катализа ферментами, поскольку открытые системы с ферментами можно рассматривать как простые модели клеточных реакций [366-371]. Физическими моделями процессов являются проточные реакторы с иммобилизованными ферментами. Степень идеализации моделей и соответственно степень приближения к реальной ситуации может варьироваться в широких пределах. Безусловно, развитые на этой основе теоретические методы найдут широкое применение для анализа действия клеточных ферментов.

Для исследования кинетики действия ферментов в открытых системах нашли применение следующие типы реакторов:

1. Проточный безградиентный реактор (проточный реактор идеального перемешивания). Существенной особенностью этого типа реакторов является идеальное перемешивание компонентов реакции, так что отсутствуют градиенты веществ внутри реакционного объема.

2. Проточный реактор с идеальным вытеснением. Этот тип реактора представляет собой объем, равномерно заполненный ферментом, в который с постоянной скоростью подается раствор субстрата. При этом в стационарном состоянии устанавливается постоянный градиент субстрата и продукта реакции, который определяется скоростью потока вводимого субстрата.

3. Мембранный реактор. Это замкнутый объем с ферментом, массоперенос субстрата в который осуществляется путем диффузии его через полупроницаемую мембрану постоянной толщины. С точки зрения биологической кинетики наиболее интересны реакторы именно этого типа. В данной главе рассмотрена кинетика действия ферментов в клетках. При этом в первом приближении клетка рассматривается как мембранный микрореактор.

Для проведения реакции с иммобилизованными ферментами используют и реакторы других типов. Достаточное развитие получили, например, трубчатые реакторы, в которых ферменты иммобилизованы на внутренней поверхности полого капилляра [372, 373]. Математическое описание трубчатого реактора и сравнение трубчатых реакторов с проточными реакторами с вытеснением и перемешиванием дано в работах [373-375].

Рассмотрим некоторый элементарный объем, в котором протекает катализируемая ферментом химическая реакция. Если субстрат ферментативного превращения помимо химической реакции способен по какому-либо закону обмениваться с окружающей средой, скорость изменения его концентрации описывает дифференциальное уравнение

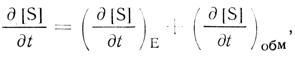(2.101)

где (∂[S]/∂t)_E - скорость ферментативной реакции; (∂[S]/∂t)_обм - скорость материального обмена.

Как скорость ферментативной реакции, так и скорость материального обмена являются функциями концентрации субстрата в данном элементарном объеме.

Участие в механизмах ферментативных реакций промежуточных соединений для большинства ферментов в растворе приводит к следующей зависимости стационарной скорости реакции от концентрации субстрата (уравнение Михаэлиса):

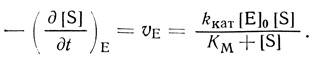(2.102)

Для ферментов в гетерогенных системах, если процесс протекает в кинетическом режиме, зависимость скорости реакции от концентрации субстрата будет иметь тот же вид. Однако для гетерогенных систем параметры k_кат и K_М часто имеют эффективный характер и осложнены кинетическими или равновесными эффектами влияния матрицы на микроокружение активных центров ферментов.

В данном разделе кинетика ферментативных реакций в открытых системах анализируется для наиболее важного случая, когда ферментативная реакция протекает в кинетическом режиме.

Скорость обмена субстрата с окружающей средой, входящая в исходное уравнение, в общем случае может быть достаточно произвольной функцией концентрации субстрата.

Рассмотрим две наиболее важные системы, в которые субстрат вводится с постоянной скоростью

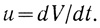(2.103)

1. Введение субстрата происходит за счет вытеснения эквивалентного элементарного объема из реакционной зоны. При этом условии

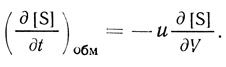(2.104)

Дифференциальное уравнение, описывающее кинетику процесса, принимает вид

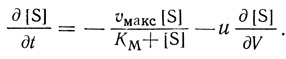(2.105)

Это уравнение реактора с идеальным вытеснением.

2. Если концентрация субстрата по всему объему постоянна и введение его в реакционную зону осуществляется с постоянной объемной скоростью u в концентрации [S]₀, скорость обмена субстрата с окружающей средой задается уравнением

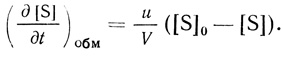(2.106)

При этом условии отсутствуют градиенты концентрации субстрата внутри объема V. Это может быть достигнуто либо путем эффективного конвективного перемешивания, либо (для микрореакторов) путем эффективного диффузионного перемешивания (так называемый случай "бесконечных коэффициентов диффузии" [376]). Дифференциальное уравнение реактора имеет вид

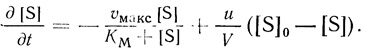(2.107)

Аналогичное уравнение описывает кинетическое поведение микрореакторов с диффузионным переносом через полупроницаемую мембрану

(2.108)

где A - поверхность мембраны; V - объем мембранного реактора; D - коэффициент диффузии субстрата в мембране; l - толщина мембраны. Ниже дано кинетическое описание и сравнение этих основных типов каталитических открытых систем с участием ферментов.

Обзор кинетических закономерностей ферментативных реакций в открытых системах дан нами в монографии [15]. Анализируются реакции в ферментативном реакторе идеального вытеснения, проточном ферментативном реакторе с перемешиванием. Дальнейшее развитие теории "идеальных" ферментативных реакторов связано с анализом кинетических закономерностей реакций в нестационарных режимах [377, 378]. Проанализировано нестационарное поведение безградиентного реактора в нестационарном режиме при импульсном и непрерывном введении субстрата [378]. Проведено сравнение реакторов различного типа с точки зрения эффективности конверсии вещества [377].