П.2.8.1. Характеристики расположения относительно центра

Среднее (среднее арифметическое)

Это "средняя величина" группы значений, которую получают путем сложения всех значений и деления суммы на число сложенных значений. Например, среднее (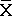) для значений x₁, x₂, х₃, х₄ ... х_n подсчитывается следующим образом:

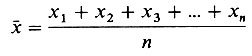
или

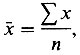
где ∑ - сумма или общее количество, х - отдельное значение и n - число отдельных значений.

Если одно и то же значение х встречается более чем один раз, среднее (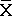) можно подсчитать, используя выражение:

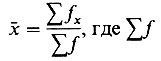
∑ƒ сумма частоты встречаемости х, или проще - n.

Медиана

Она представляет собой среднее, или центральное, значение группы переменных. Например, если пять значений х расположены в следующей последовательности: x₁, x₂, х₃, х₄ и х₅, то значение медианы будет равно х₃, так как равное число значений расположено до и после х₃. Если число значений четное, например от x₁ до х₆, то медиана будет равняться среднему из двух срединных значений

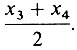
Мода

Это значение переменной, встречающееся наиболее часто. Например, если число детей в десяти семьях соответственно равно 1, 1, 1, 2, 2, 2, 2, 3, 4, то мода равна 2.

Каждое из трех значений, описанных выше, имеет свои преимущества и недостатки и применяется при решении определенных задач. Проиллюстрировать применение среднего или моды можно на примере с различным числом детей в семьях. Среднее число детей в семье составляет 2,4, но так как ребенок - величина дискретная, естественно описывать число детей в семье в целых числах, т. е. с помощью моды, которая равна 2.

В случае нормального распределения значения среднего, медианы и моды совпадают (рис. П.2.15, А). В случае того или иного уклона частоты распределения их значений не совпадают (рис. П.2.15, Б).

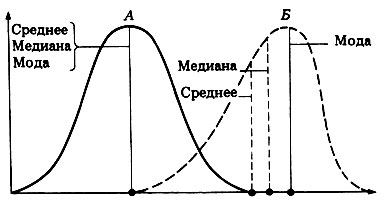
Рис. П.2.15. Положение среднего, медианы и моды при нормальном распределении (А) и при распределении с уклоном (Б)