П.2.8.2. Оценки дисперсии

Для того чтобы оценить, в какой мере значения признака отклоняются от среднего, вычисляют среднее и дисперсию. Для нормального распределения это проиллюстрировано двумя кривыми на рис. П.2.16. При статистическом анализе данных очень информативной является оценка среднего квадратичного или стандартного отклонения; по этим показателям можно предсказать и распределение значений вокруг среднего, и ответить на вопрос, достоверна ли разница между двумя группами данных.

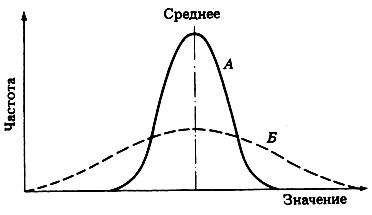
Рис. П.2.16. Две кривые нормального распределения, демонстрирующие распределение двух совокупностей данных (возможно, характеризующих популяцию) с одинаковой общей частотой (т. е. площади под кривыми равны). Кривая А построена по ограниченному ряду значений, сгруппированных вокруг среднего. Кривая Б построена по широкому ряду значений, не сгруппированных вокруг среднего

Стандартное отклонение

Стандартное отклонение (s) совокупности данных служит мерой отличия этих данных от среднего арифметического. Для его подсчета используют выражение:

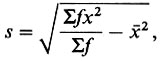
где ∑ - сумма, ƒ - частота, х - отдельные значения и 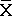- среднее. Например, в выборке из десяти раковин блюдечка (Patella vulgaris), отобранных на скалистом берегу, эти раковины имеют следующие максимальные значения диаметров в миллиметрах: 36, 34, 41, 39, 37, 43, 36, 37, 41, 39. Чтобы определить среднее максимальное значение диаметра и стандартное отклонение, необходимо вычислить ƒ, ƒx₂ и х^-2, как это показано в следующей таблице:

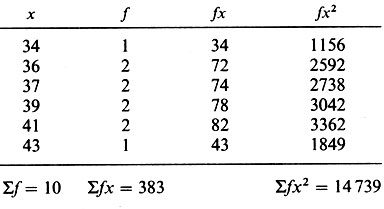
Таблица

Следовательно, 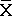=38,3; х^-2=1466,9,

Так как

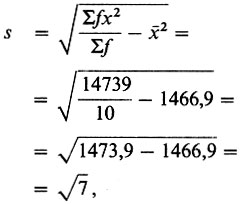
Следовательно, s = 2,65.

В этой популяции имеющих общее происхождение блюдечек среднее максимальное значение диаметра раковины равно 38,3 мм, а стандартное отклонение равно 2,7 мм (округлили до одной десятой). Если эти значения применить к более крупной популяции блюдечек общего происхождения, то на основе статистики можно предположить, что приблизительно 68% популяции будет иметь диаметр раковины 38,3 мм плюс-минус одно стандартное отклонение (2,7 мм), т. е. размеры раковин будут лежать в интервале от 35,6 до 41,0 мм; приблизительно 95% популяции будут иметь диаметр раковины 38,3 мм плюс-минус два стандартных отклонения (5,4 мм), т. е. диаметры будут лежать в интервале 32,9-43,7 мм, а практически 100% будут лежать в интервале плюс-минус три стандартных отклонения от 38,3 мм.

По величине стандартного отклонения можно судить о разбросе данных. Если стандартное отклонение мало, то, следовательно, разброс (отклонение от среднего) невелик и популяция в значительной степени однородна, как это показано на рис. П.2.16, А С увеличением стандартного отклонения увеличивается степень изменчивости внутри популяции, как показано на рис. П.2.16,2?.

Дисперсия

Дисперсия - это квадрат стандартного отклонения. Дисперсия совокупности значений подсчитывается по следующей формуле:

Дисперсия

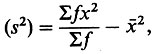
где ƒ - число значений в совокупности.

Дисперсию обычно подсчитывают в экологических исследованиях, включающих изучение питания, размножения и поведения, поскольку она служит показателем распределения организмов внутри популяции. Распределение может быть:

а) случайным;

б) групповым;

в) регулярным.

Для того чтобы определить тип распределения организмов внутри популяции, исследуемую площадь делят на квадраты равного размера (см. разд. 13.2) и подсчитывают число организмов этой популяции в каждом квадрате. Исходя из этих данных, подсчитывают значение дисперсии по следующей формуле:

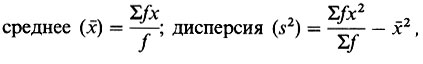
где ƒ - число квадратов, содержащих х организмов. Используя выражение:

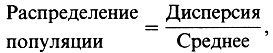
Можно выделить три типа распределения (рис. П.2.17).

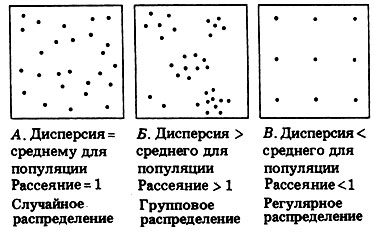
Рис. П.2.17. Типы распределения