П.2.8.3. Связь между переменными

Данные всегда необходимо представлять таким образом, чтобы можно было выявить связи между двумя или более их совокупностями. Проще всего это сделать с помощью графика или диаграммы, показывающих связь между переменными. Но это целесообразно только в том случае, если одна из переменных (независимая переменная) находится под контролем экспериментатора, как, например, в случае, приведенном на рис. П.2.8.

В других случаях, когда обе переменные являются независимыми, составляют таблицу, в которой значение одной помещают под соответствующим значением другой, как, например, в случае данных о росте и массе 20 студентов шестого курса, приведенных на рис. П.2.18, А. На основе этих данных вычерчивают график (рис. П.2.18, Б), который называется диаграммой рассеяния. По внешнему виду графика видно, что эти две переменные связаны между собой некоторым образом, но эту связь невозможно описать более точно до тех пор, пока они не будут представлены в виде прямой линии, проходящей через точки графика.

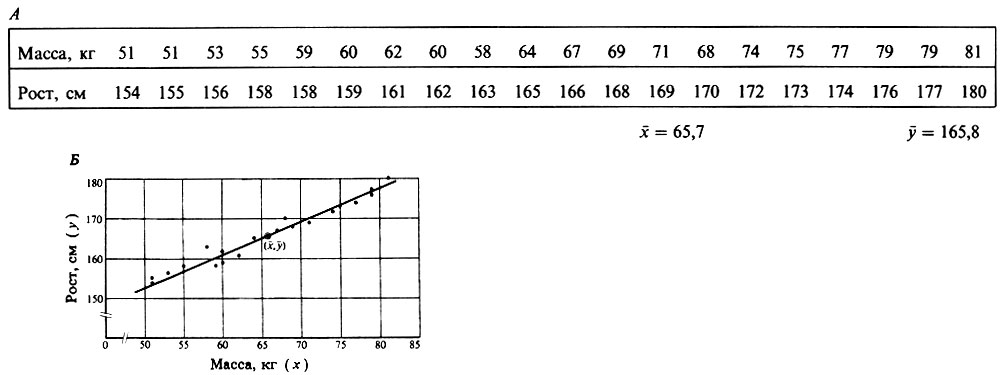
Рис. П.2.18. Данные о массе и соответствующем росте 20- и 16-летних студентов мужского пола представлены в виде таблицы (А) и диаграммы рассеяния (Б). Построена кривая регрессии

Эта линия называется "линией наибольшего соответствия", или линией регрессии. Мера приближения точек к линии указывает на степень корреляции между двумя переменными. Линия наибольшего соответствия должна проходить через точку, соответствующую среднему значению массы и роста (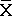=65,7 кг, 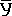=165,8 см), а число точек над и под линией должно быть приблизительно одинаковым. По этой линии можно подсчитать рост, соответствующий определенной массе.

Корреляция

Описанную выше связь между двумя переменными х и у можно обозначить термином корреляция. Между х и у могут существовать различные степени корреляции, как это показано на диаграммах рассеяния на рис. П.2.19.

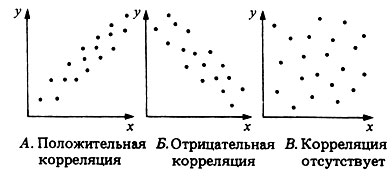
Рис. П.2.19. Типы корреляции; А - положительная корреляция; Б - отрицательная корреляция; В-корреляция отсутствует

С помощью диаграммы рассеяния нельзя точно продемонстрировать значимость между совокупностями данных, так как этот способ субъективен. Значимость корреляции можно представить с помощью статистического критерия, называемого коэффициентом корреляции. Его величина может изменяться от -1 до +1; -1 означает полностью отрицательную корреляцию, например отрицательную корреляцию между давлением кислорода в атмосфере и скоростью открывания дыхалец у насекомых; 0 означает отсутствие корреляции, например отсутствие корреляции между размерами плодов томатов и числом семян; +1 означает полностью положительную корреляцию, например положительную корреляцию между возрастом и длиной тела у саранчи.