Рентгеноструктурные исследования монокристаллов

Прежде чем приступить к описанию некоторых чрезвычайно важных аспектов применения рентгеновской кристаллографии в химии и биологии, необходимо познакомиться с принятой в этой области терминологией и принципами метода. Как указывалось выше, рентгеновские лучи можно использовать потому, что их длина волны достаточно мала (~1 Å), а это и позволяет получить высокое разрешение молекулярной структуры.

Определим кристалл как трехмерное множество или решетку, состоящую из регулярно повторяющегося пространственного мотива. Мориц Эшер предложил графическое изображение решетки, приведенное на рис. 10.1. Наименьший элемент пространственной структуры, повторением которого можно получить решетку, обычно называют элементарной ячейкой.

Рис. 10.1. Изображение решетки, называемой 'кубическое деление пространства'

Сама дифракционная картина также представляет собой изображение решетки, в которой расстояния между узлами (рефлексами) не являются случайными. Они связаны с расстояниями между узлами в истинной кристаллической решетке. Интенсивности рефлексов описываются сложными математическими уравнениями для рассеяния на регулярно расположенных атомах. Имеется общий математический принцип, гласящий, что для представления периодической функции могут применяться ряды Фурье. Ряд Фурье такой функции определяется 1) частотой синусоидальных и косинусоидальных волн и 2) их амплитудой. Синтез Фурье применим, если исходная функция может быть восстановлена суммированием амплитуд синусов и косинусов.

Поскольку кристалл периодичен в пространстве в трех направлениях, электронную плотность его можно представить трехмерным рядом Фурье:

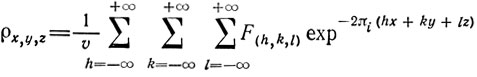
где p_x,y,z - электронная плотность в каждой точке элементарной ячейки, v - объем элементарной ячейки, а h, k и l - компоненты волнового числа для данной синусоидальной волны по всем основным осям кристалла. F_(h,k,l) - коэффициент Фурье или структурная амплитуда является комплексным числом, определяемым модулем и фазой (рис. 10.2). Каждой точке дифракционной картины по идее соответствует член представления Фурье. Соответствующая интенсивность пропорциональна квадрату структурной амплитуды.

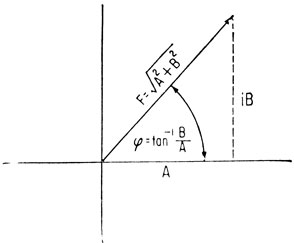
Рис. 10.2. Графическое представление вектора структурной амплитуды, иллюстрирующее, что она определяется действительной (A) и мнимой (iB) компонентами, или, что то же самое, модулем F и фазовым углом φ

Из дифракционной картины нельзя получить информацию, позволяющую связать фазу каждой волны с фазами остальных волн. Важность значения фаз можно представить из рис. 10.3 (взятого из обзора Дикерсона [1]), на котором показано сложение двух совпадающих и сдвинутых по фазе волн.

Рис. 10.3. Синтез Фурье - сложение волн и эффект сдвига по фазе. (a) - (c). Построение периодической функции путем сложения синусоидальных функций: (а) f(x)=10 sin2πx; (b) f(x)=-5 cos2π(2x); (c) f(x)=10 sin2πx -5 cos2π(2x). Функцию 'с' можно представить как одномерное сечение структуры, где атом соответствует пику, помеченному стрелкой. (d) - (f). Влияние сдвига по фазе одного из членов на синтез Фурье. Функция 'b' сдвинута на четверть периода тогда: (d)f(x)=10 sin2πx; (e)f(x)=-5 cos2π(2x+sup1/sup/sub4/sub)=+5 sin2π(2x); (f) f(x)=10 sin 2πx-5 cos2π(2x+sup1/sup/sub4/sub). Такая картина уже не похожа на профиль атома. Общий характер синтеза Фурье радикальным образом искажается вследствие изменения относительных фаз составляющих его волн [1]

Основная трудность для кристаллографов состоит в решении фазовой проблемы. Для того чтобы показать, почему необходимо знать фазы дифрагирующих волн, полезно применить аналогию с оптическим изображением.

На рис. 10.4 приведены изображения объекта (утки) и его трансформация объективом оптической камеры. В части рисунка, обозначенной буквой а, мы видим, как единственная утка превращается в ряд неровных концентрических колец, на которых форма и детали утки не различимы. Интенсивность этих колец зависит от плотности вещества, из которого состоит утка. В той части рисунка, которая обозначена буквой б, мы видим двух уток, находящихся на расстоянии x друг от друга. Оптическая трансформация этого объекта имеет вид концентрических колец, состоящих из отдельных пятен, причем расстояние между пятнами в каждом из колец составляет 1/x. И в данном случае детали уток исчезли. Наконец, в части рисунка, обозначенной буквой в, изображены четыре утки, находящиеся друг от друга на расстояниях x и y. Оптическая трансформация вновь дает пятна (а не самих уток), из расположения которых можно определить расстояния 1/x и 1/y. Расстояния, получаемые в оптической трансформации, являются величинами, обратными реальным расстояниям между элементами объекта в пространстве. Периодичность оптической трансформации обратна периодичности решетки кристалла. Если восстановить реальные расстояния, используя фурье-представление и не учитывая сдвиг по фазе, мы получим пятна, отделенные друг от друга правильными расстояниями, но не получим изображения уток. Метод восстановления изображения уток в общем аналогичен методу установления структуры кристалла по дифракционной картине.

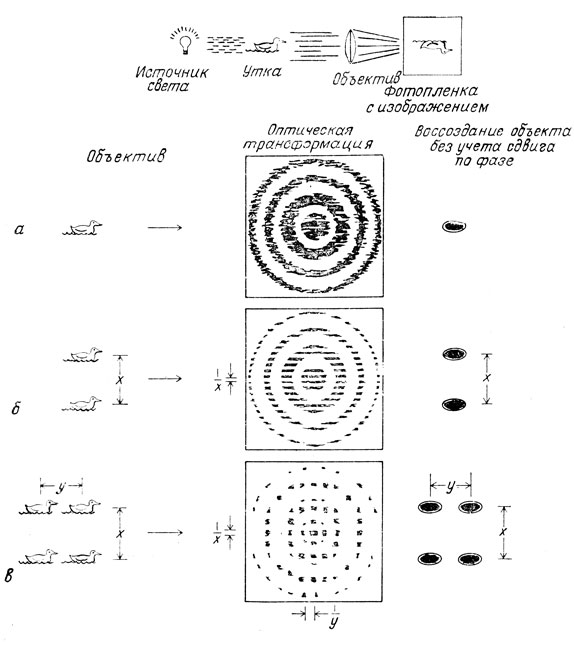
Рис. 10.4. Оптическая аналогия дифракции рентгеновских лучей. Оптическая трансформация представляет собой распределение интенсивности света различных длин волн, рассеиваемого объектом, при прохождении через объектив. Объектив не меняет относительного фазового сдвига между разными длинами волн света, рассеиваемого уткой (верхняя часть рисунка). Благодаря тому, что световые волны, обладающие достаточно большой длиной волны, можно сфокусировать, на фотопленке удается получить изображение утки. Однако если бы произвести сдвиг световых волн по фазе, а затем попытаться восстановить изображение уток, получилось бы просто пятно. Из-за того, что коротковолновое рентгеновское излучение сфокусировать не удается (показатель преломления для рентгеновских лучей равен единице для всех веществ), основной и главной задачей при установлении структуры молекул является правильное определение сдвига по фазе

При установлении структуры любого вещества первым шагом является определение размера и формы элементарной ячейки и числа молекул, входящих в эту ячейку. После этого проводят поиск "систематических погасаний" дифракционных пятен (или рефлексов).

Оптическая трансформация представляет собой распределение интенсивности света, рассеянного объектом. На верхнем рисунке сдвиг по фазе различных световых волн, рассеиваемых уткой, не меняется при прохождении через объектив. Поскольку длинноволновое излучение, соответствующее видимому свету, можно собрать (сфокусировать), на фотопленке может быть непосредственно получено изображение утки. Однако если сдвинуть световые волны по фазе и затем попытаться восстановить изображение уток, вместо них получились бы лишь, пятна. Поскольку коротковолновое рентгеновское излучение сфокусировать нельзя (показатель преломления рентгеновских лучей почти в точности равен единице для всех веществ), при воссоздании структуры самой главной и определяющей успех задачей оказывается определение сдвига по фазе для разных рефлексов. Получаемые при этом результаты позволяют отнести кристалл к соответствующей "пространственной группе".

Уравнение Брэгга, описывающее дифракцию рентгеновских лучей, имеет следующий вид:

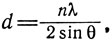
где d - расстояние между параллельными плоскостями кристалла, n - целое число, λ - длина волны рентгеновских лучей, θ - угол наклона пучка рентгеновского излучения по отношению к плоскости кристалла.

Предположим, что рассеивающие центры расположены в параллельных плоскостях на определенных расстояниях d и что каждая рассеянная волна будет находиться в фазе, взаимодействуя с волнами, рассеянными последовательно расположенными параллельными плоскостями. В таком случае дифракционные пятна на дифракционной картине будут иметь одинаковую интенсивность. Для реальной структуры это, однако, не так. Интенсивность дифракционных пятен на рентгенограмме меняется в широком интервале. Изменения интенсивности обусловлены тем, что рассеивающие центры не расположены точно на плоскостях кристалла, а распределены во всей элементарной ячейке. Задача состоит в определении распределения рассеивающего вещества, т. е. электронов в атоме, по наблюдаемым интенсивностям рефлексов.

Следует помнить, что F(h, k, l) является комплексной величиной, в нее входит не только амплитуда, но также и фаза рассеянного луча. Наблюдаемые на дифракционной картине рефлексы позволяют рассчитывать лишь абсолютные значения интенсивностей, но не дают, к сожалению, сведений о значениях фазовых констант.

Поэтому применение синтезов Фурье для установления структуры кристаллов оказывается весьма ограниченным. Однако значение этого мощного метода для представления и уточнения результатов анализа кристаллов все еще сохраняется^*.

^* (Если кристалл имеет центр симметрии, который принимают за начало координат, фазовые углы могут иметь значение или 0, или я. Поэтому знак коэффициента может быть либо положительным, либо отрицательным. Для структуры, обладающей центром симметрии, ряд Фурье можно записать в виде 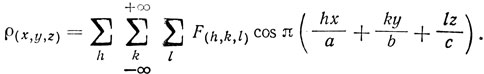В таком простом случае мы должны знать значение F_{(h, k, l)}^**.)

^** (Случай с центросимметричными кристаллами вовсе не "простой", так как если учесть, что каждая амплитуда - а их сотни и тысячи - может принимать положительные или отрицательные значения, то число вариантов становится астрономически большим. - Прим. перев.)

Метод проб и ошибок состоит в следующем: из тех или иных данных делается предположение о положении атомов. Затем рассчитывают значения F_(h,h,l). Наблюдаемые интенсивности сравнивают с расчетными. Если они согласуются достаточно хорошо, их можно использовать для расчета электронной плотности. Составленная карта электронной плотности будет иметь максимумы, положения которых немного отличаются от первоначально предполагаемых. Затем положение атомов несколько меняют и рассчитывают другой набор F_(h,k,l), который берут для расчета новых значений электронной плотности по новому синтезу Фурье. Фурье-представление прекрасно изображало бы структуру кристалла в том случае, если бы можно было с большой точностью определить все коэффициенты и фазовые константы и если бы можно было использовать бесконечно большой набор рефлексов. На практике это не так и используется лишь конечное число членов ряда, что задается экспериментальными условиями и используемой длиной волны. Успех определяется тем, близки ли предполагаемые положения атомов в каких-то точках к истинным положениям, что определяется мерой согласованности расчетных и наблюдаемых интенсивностей. Если они близки, правильные положения могут быть найдены путем небольших разумных смещений некоторых или всех атомов из первоначальных положений. Применимость такого прямого приближения резко уменьшается при увеличении размеров и сложности молекулы органического соединения. Рассматриваемый подход оказался очень ценным для кристаллических соединений низкого молекулярного веса. Структуры, полученные таким прямым методом для производных аминокислот и дипептидов, были использованы Полингом для установления структуры фибриллярных белков.

Другой путь, позволяющий обойти фазовую проблему, заключается в использовании тяжелых атомов. Производимое ими рассеяние рентгеновских лучей преобладает в дифракционной картине, если тяжелый атом содержит существенную долю всех входящих в молекулу электронов.

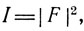
где I - интенсивность рассеяния, а |F|² - квадрат амплитуды волны, определяемой электронной плотностью. После того как установлено положение тяжелого атома, фазу его можно вычислить, применяя разложение в ряд Фурье. При этом предполагают, что структура целиком состоит из тяжелого атома, что, конечно, не отвечает истине, но является достаточно близким приближением, позволяющим обнаружить некоторые отчетливые детали структуры. Для большинства рефлексов фаза, отвечающая рассеянию целой молекулой, не очень отличается от рассеяния одного лишь тяжелого атома. Рассчитанные фазы тяжелого атома объединяют с наблюдаемыми интенсивностями, чтобы получить фурье-представление. Такая операция дает приближенную структуру. Если удается установить положения некоторых легких атомов, их используют для уточненного расчета фазовых факторов, которые затем вновь используют для фурье-представления. Истинную структуру можно получить, проводя последовательно уточнение фазовых отношений и расчет соответствующих фурье-представлений (рис. 10.5).

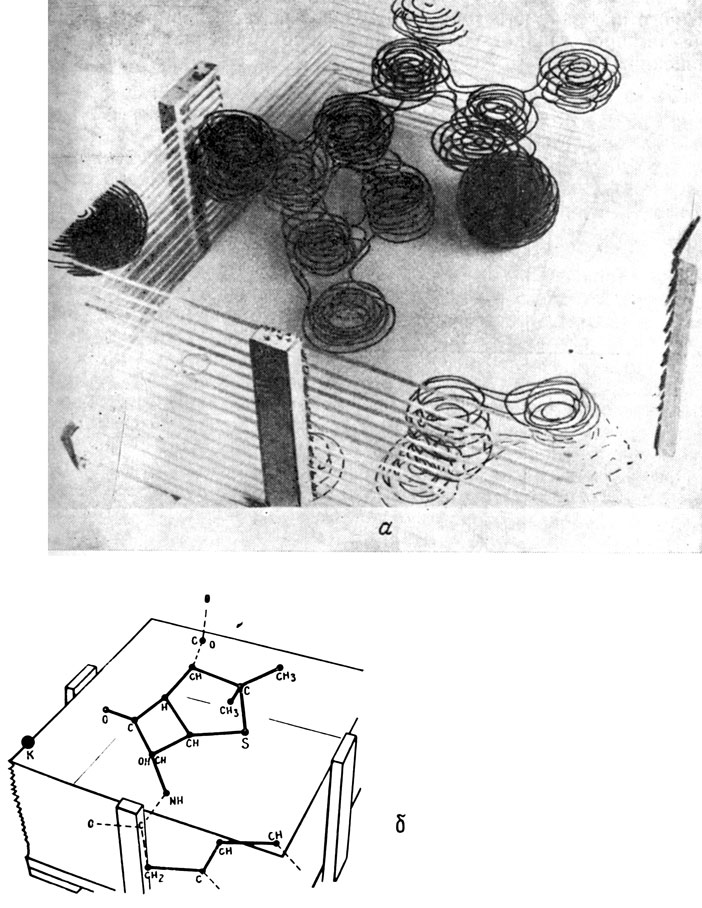
Рис. 110.5. а - модель распределения электронной плотности Калийбензилпенициллина, изображенная с помощью контуров линий равной электронной плотности на листаж из плексигласа, б - атомная структура соединения на основании приведенной на рис. а модели

Так как размеры белковых молекул весьма велики, то нет настолько тяжелых атомов, рассеяние на которых могло бы преобладать в картине рентгеновской дифракции. Для установления структуры белков необходимо применять метод многократного изоморфного замещения, получая кристаллы по крайней мере двух производных с тяжелыми атомами, для которых введение тяжелого атома не изменяет геометрию кристалла белка и строение самой белковой молекулы (изоморфное замещение).

Рентгенограммы молекул белков, замещенных и не замещенных тяжелым атомом, отличаются чрезвычайно мало. Общее рассеяние (F_H) представляет собой сумму рассеяния белком и тяжелым атомом (f):

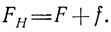
Измеряют интенсивности дифракционных отражений для исходного кристалла и для кристаллов, содержащих тяжелый атом. Нахождение фаз сводится к решению тригонометрической задачи об определений ориентации треугольника, получаемого при суммировании векторов, в соответствии с вышеприведенным уравнением. Для одного производного белка с тяжелым атомом существуют два фазовых угла, удовлетворяющих векторному уравнению. Для второго производного, в которое введен другой тяжелый атом, также есть два решения, одно из которых совпадает с ориентацией векторов для одного из решений, полученного для первого изоморфного производного (рис. 10.6). Фазовый угол, общий для двух решений, представляет собой правильное решение векторного уравнения.

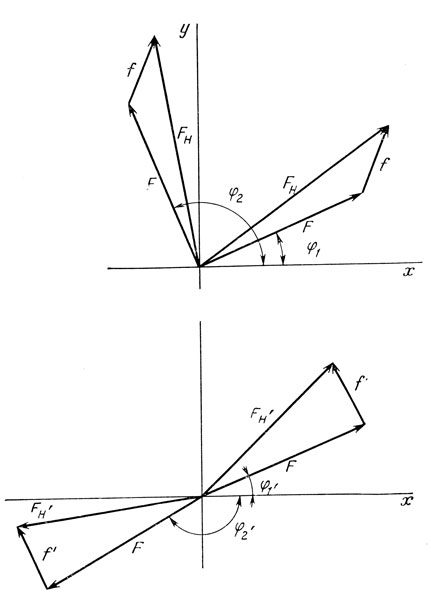
Рис. 10.6. Изображение векторных диаграмм, иллюстрирующих необходимость многократного изоморфного замещения в общем случае. Значения структурных факторов для исходного белка F и производных, полученных при замещении тяжелыми атомами (F_Н и F_Н′), являются наблюдаемыми векторами. Для обоих производных можно рассчитать величину и ориентацию вклада, вносимого только тяжелым атомом f и f′. Для каждого производного из этих векторов можно построить по два замкнутых треугольника. Общим для обоих производных является только один угол, истинный фазовый угол близок к значениям φ1 и φ′₁

Значительные ошибки, возникающие при определении положения атомов и при измерениях интенсивностей для кристаллов белков и их производных, определяют необходимость применения метода изоморфного замещения к более чем двум производным с тяжелыми атомами. Для проведения структурного анализа белков необходимо собрать большое число интенсивностей дифракционных отражений. В настоящее время применяют автоматический контроль за сбором данных при помощи ЭВМ. Установка и вращение кристалла производятся автоматически, интенсивности всех рефлексов хранятся в памяти ЭВМ. С помощью ЭВМ производят расчет синтезов Фурье, а также уточнение найденной структуры.

Наиболее важен в этом методе подбор подходящих производных, содержащих один тяжелый атом на молекулу. Если такие производные изучаемого соединения получены, установление его пространственной структуры является лишь вопросом времени и затраты труда. Изоморфные кристаллы белка можно получить тремя методами:

1) химической модификацией белка с последующей его кристаллизацией, если соединение с тяжелым атомом относится к такому типу соединений, которые вступают в определенные химические реакции;

2) кристаллизацией в присутствии соединения с тяжелым атомом, не образующего ковалентных связей;

3) диффузией соединения с тяжелым атомом в кристалл белка. Все три подхода основаны на использовании метода проб и ошибок. Общей методики или принципов, которым нужно следовать для того, чтобы приготовить изоморфнозамещенные тяжелыми атомами производные сложных органических соединений, пригодные для успешного рентгеноструктурного исследования, не существует.

На основании приведенного выше материала вырисовывается следующая схема последовательности операций, применяемых при изучении структуры глобулярных белков: а) получение хороших кристаллов; б) получение по крайней мере двух изоморфнозамещенных тяжелыми атомами производных; в) измерение интенсивности дифракционных отражений для кристаллов исходного белка и белка, содержащего тяжелые атомы; г) расчет фазовых углов всех рефлексов (как показано на рис. 10.6); д) расчет синтеза Фурье по вычисленным значениям фазовых углов и интенсивностям рефлексов (первое приближение распределения электронной плотности в белковой молекуле); е) построение исходной модели; ж) повторный расчет уточненных значений фазовых углов; з) повторный синтез Фурье; и) построение уточненной модели и т. д.