Цепные макромолекулы

До сих пор рассматривались основные принципы рентгеновской кристаллографии и рентгеноструктурного исследования монокристаллов. Волокна представляют собой другой тип упорядоченных молекулярных образований. Обычно рентгеновское излучение направляют через кристаллическое или частично кристаллическое волокно перпендикулярно его оси. Получаемую при этом дифракционную картину используют для расчета некоторых параметров молекулы волокна, например периода идентичности. Термин "кристалличность" применительно к волокнам характеризует порядок внутри полимерных цепей и регулярность их упаковки. Теоретически волокно может иметь строгий трехмерный порядок, если регулярно построенные бесконечно длинные цепи будут правильным образом упакованы в направлении, перпендикулярном их осям. Реально существующие полимеры могут обладать лишь частичной кристалличностью, так как наличие концевых групп макромолекул, обусловленное их конечной длиной, приводит к дефектам упорядоченности их упаковки. При растяжении многие волокна цепи становятся ориентированными, что приводит к существенному возрастанию кристалличности вдоль оси растяжения. Механическая ориентация сравнительно слабо влияет на силы, обусловливающие упаковку цепей, и обычно в направлении, перпендикулярном осям макромолекул, наблюдаются значительные по размеру области, в которых упорядоченность отсутствует. Такие системы, состоящие из кристаллических областей (кристаллитов) и неупорядоченных областей (аморфных зон), дают дифракционные картины, состоящие из рефлексов в виде размытых дуг, располагающихся вокруг следа первичного пучка. В результате менее высокой упорядоченности волокна дают рентгенограммы с гораздо меньшим числом рефлексов, чем монокристаллы. К сожалению, аморфные области дают фон рассеянного излучения, который может препятствовать правильной интерпретации рентгенограмм волокон.

Расшифровка картин дифракции рентгеновских лучей волокнами основана на том, что местонахождение и интенсивность дифракционных пятен прямо связаны с особенностями структуры волокна. Вертикальная линия, проходящая через центр рентгенограммы, называется меридианом, а горизонтальная линия, проходящая через эту точку - экватором (рис. 10.12). Рефлексы на меридиане дают сведения о порядке вдоль оси волокна, экваториальные рефлексы отражают упорядоченность в перпендикулярном направлении.

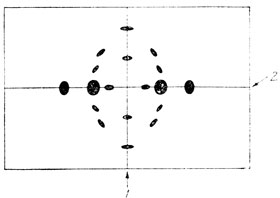
Рис. 10.12. Схематическое изображение части рентгенограммы волокна, установленного перпендикулярно направлению рентгеновского излучения. 1 - меридиональная ось рентгенограммы; 2 - экваториальная ось рентгенограммы

Рефлекс, расположенный на меридиане на расстоянии d′ от центра, характеризует реальный период идентичности d вдоль оси волокна:

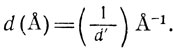
Это было давно установлено К. Майером и Г. Марком, которые первыми начали исследование рентгенограмм волокон. Они изучали фиброин шелка и обнаружили меридиональные рефлексы при d′=0,143 Å^-1, соответствующие периоду идентичности вдоль оси волокна, равному 7 Å (рис. 10.13). Марк предположил, что это расстояние как раз достаточно для повторения двух полностью вытянутых аминокислотных звеньев (рис. 10.14). Кроме того, имеется очень интенсивный рефлекс при d′=0,285 Å^-1 на меридиане, что соответствует периоду 3,5 Å, достаточному для одного полностью вытянутого аминокислотного звена. Оба эти рефлекса соответствуют структуре полностью растянутых полипептидных цепей. Так была раскрыта структура β-формы белков. Астбэри, используя экваториальные рефлексы, выяснил упаковку β-кератина (белка, образующего кожу, волосы и т. д.). Он приписал вычисленную по рентгенограмме величину 4,65 Å расстоянию между полипептидными цепями, находящимися в одной плоскости и связанными водородными связями, а величину 9,8 Å - расстоянию между плоскостями, образованными полипептидными цепями (рис. 10.15).

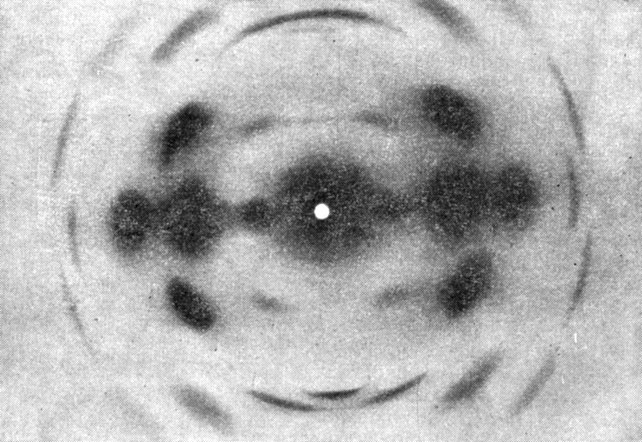
Рис. 10.13. Дифракционная картина фиброина шелка. Хорошо видны интенсивные меридиональные рефлексы

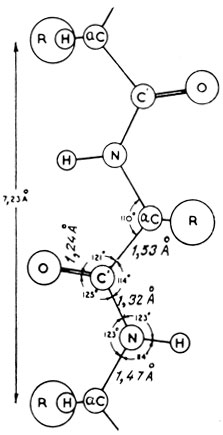
Рис. 10.14. Схема полностью растянутой полипептидной цепи, для которой расстояние между аминокислотами составляет 7,23 Å

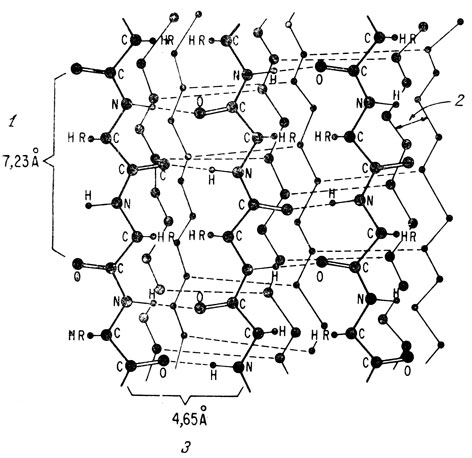
Рис. 10.15. Слои, образованные полностью вытянутыми полипептидными цепями, характерные для шелка, волос и т. д. Анализ рефлексов на рентгенограммах (рис. 11.12) дает указанные на рисунке межплоскостные и межцепочечные расстояния, а также период идентичности вдоль цепи. 1 - период идентичности вдоль цепи 7,23 Å; 2 - межплоскостное расстояние 9,8 Å; 3 - межцепочечное расстояние 4,65 Å

Как можно видеть из рентгенограммы волокна, приведенной на рис. 10.13, рефлексы располагаются только вдоль слоевых линий. Кристаллографический период идентичности дает рефлексы, находящиеся от центра рентгенограммы на расстояниях, кратных d′:

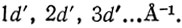
Эти числовые коэффициенты называют порядками межплоскостных расстояний d реальной структуры.

Большинство упорядоченных волокнистых структур образуется не из растянутых полимерных цепей. Это является следствием особенностей упаковки или природы боковых групп, выступающих за пределы главной цепи. Так, например, линейный полиэтилен можно описать как вытянутую зигзагообразную структуру (рис. 10.16), но изотактическому полипропилену (гл. 4) такую структуру приписать нельзя, поскольку в этом случае при полностью растянутой цепи атомы одной метальной группы попадали бы в пространство, занимаемое другой метальной группой. Единственным способом упорядочения структуры в таких полимерах является образование спирали. И действительно, большинство упорядоченных полимеров винилового ряда в твердом состоянии состоит из молекул, имеющих форму спиралей.

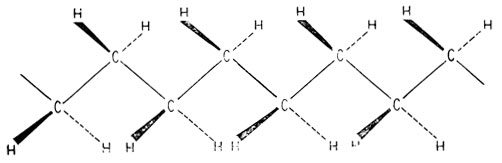
Рис. 10.16. Линейный полиэтилен в форме плоского зигзага транс-конфигурации

Биополимеры также образуют спирали. Большинство фибриллярных белков и нуклеиновых кислот относится к полимерам со спиральной симметрией. Период идентичности включает вращение и трансляцию вдоль оси спирали.

Полинг ввел "постулат эквивалентности", согласно которому все мономерные звенья занимают геометрически идентичные положения относительно кристаллографического направления, совпадающего с осью макромолекулы. Поскольку α-аминокислотные остатки не имеют элементов симметрии, единственным способом, позволяющим превратить координаты одного аминокислотного остатка в координаты другого такого остатка, является винтовой перенос (перенос с поворотом) вдоль оси цепи. Такая операция приводит к образованию спиральной структуры. Говорят, что спираль, содержащая n повторяющихся звеньев в витке, имеет винтовую ось n-го порядка.

При изучении белков Полинг рассматривал лишь структуры с плоской транс-конфигурацией пептидной связи. Такое представление разумно с точки зрения резонанса, а также согласуется с рентгеноструктурными данными, полученными для монокристаллов таких соединений, как N-ацетилглицин, глицилглицин, D, L-аланин и L-треонин.

Эти данные полностью соответствуют общей картине вытянутой поли-α-аминокислотной цепи, обсуждавшейся выше. Водородные связи между амидной NH-группой и карбонилом в основном являются линейными, хотя допускаются некоторые отклонения от такой линейности. На основании этих исследований были получены новые данные, позволившие объяснить спиральную структуру белков.

Ограничения, накладываемые требованиями транс-планарного расположения амида, определенной длины связей и величины углов, линейности и длины водородной связи, а также постулатом эквивалентности, приводят к тому, что им может соответствовать лишь ограниченное число поворотов на аминокислотный остаток. Всем этим требованиям удовлетворяет практически лишь поворот на 97,2°. Полинг назвал структуру, получающуюся в результате такого поворота цепи, α-спиралью (рис. 10.17). В α-спирали последовательно расположенные аминокислотные остатки смещены в аксиальном направлении примерно на 1,5 Å; шаг спирали составляет около 5,4; на один виток приходится 3,67 аминокислотных остатка, а линия, соединяющая карбонильные и NH-группы, образующие водородные связи внутри цепи, образует с осью спирали угол 12° (рис. 10.18).

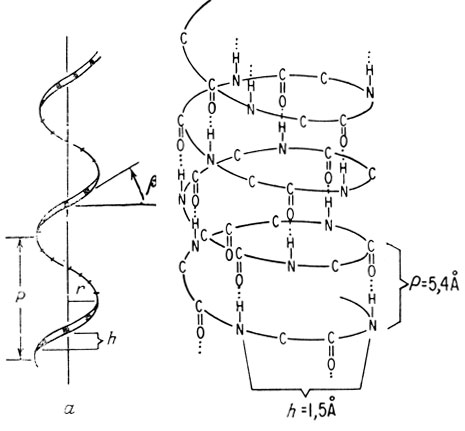
Рис. 10.17. Схематическое изображение простой спирали (а) и α-опирали (б). P - шаг спирали; r - радиус спирали; h - аксиальное смещение на аминокислотный остаток; β - угол наклона витка спирали; n - число повторяющихся единиц на один оборот спирали

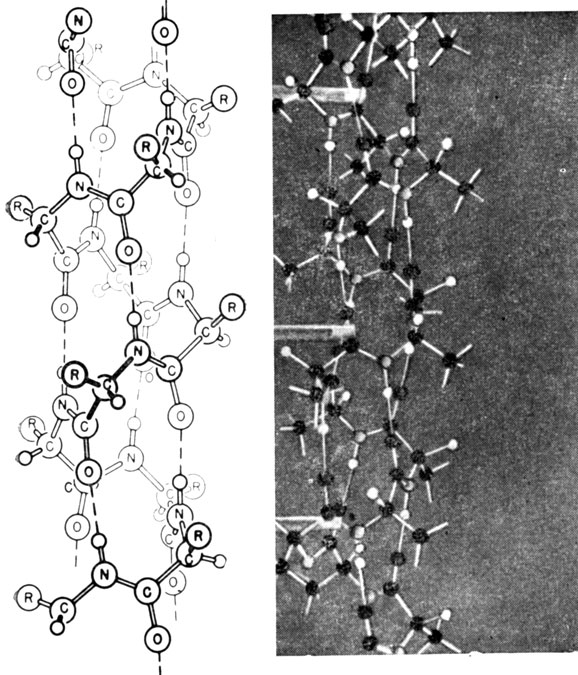
Рис. 10.18. Модель α-спирали

Вскоре после предсказания Полингом строения α-спирали Перутц получил экспериментальное подтверждение существования правой α-спирали, обнаружив период 1,5 Å для цепи синтетического полипептида, а также α-кератина и гемоглобина. Впоследствии было показано, что правая α-спираль^* является общим элементом для многих других белков.

^* (Определение спирали зависит от направления поступательного движения вдоль скелета цепи. Спираль называют правой, если поступательное движение идет по часовой стрелке.)

После того как Полингом была предложена α-спираль в качестве пространственной модели структуры белка, несколько групп исследователей занялись изучением деталей рентгенограмм спиральных структур. Для описания спиральных структур пользуются Цилиндрическими координатами (рис. 10.19, б). Дифракционные пятна ограничены значениями Z=l/P где l - номер слоевой линии, который может иметь положительные, отрицательные или нулевые значения, а P - это шаг спирали (рис. 10.17).

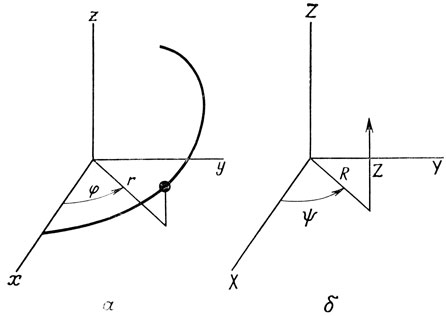
Рис. 10.19. Цилиндрические координаты, описывающие спиральные структуры (а) и рентгенограммы таких структур (б). r (радиус спирали) и x, y, z - координаты, выраженные в ангстремах, а φ - угол между плоскостью и падающим лучом. R, Z и ψ - аналогичные координаты для рентгенограммы

Если спираль обладает периодом повторяемости с (т. е. структура точно повторяется при изменении координаты вдоль оси спирали на величину с) и расстоянием, для которого целое число оборотов опирали равно N, а целое число мономерных звеньев равно M, то справедливо следующее соотношение:

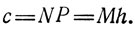
Дифракционную картину можно объяснить на основании того, что Z=l/c.

Рассмотрим α-спираль, в которой 18 аминокислотных остатков повторяются после 5 витков (или на виток приходится 3,67 остатка), а период по оси составляет 27 Å:

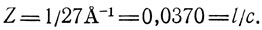
Индексация слоевых линий такой структуры приводит к тому, что первый рефлекс на меридиане относят к 18-му слою. Небольшое изменение наклона приводит к существенным изменениям, которых следует ожидать для значений Z. Спираль, в которой на один виток укладывается 3,61 аминокислотных остатка, дала бы структуру, в которой 65 остатков повторялись бы через 18 витков, занимающих расстояние 97,5 Å.

Реально существующие спирали допускают искажение шага спирали для того, чтобы могли быть соблюдены упаковочные факторы и (или) скомпенсированы дефекты.

Как же по рентгенограммам устанавливают молекулярные структуры волокон? Каждый специалист, занимающийся кристаллографией, пользуется собственным подходом, а определенный тип волокна ставит перед исследователем самостоятельную задачу. Рассмотрим в качестве отправной точки изотактический полипропилен (гл. 4). Натта и Коррадини установили структуру этого полимера лишь после интенсивного изучения путей его синтетического получения, затем они приготовили из него волокно, измерили степень кристалличности, рассмотрели геометрию и, наконец, провели подробное рентгеноструктурное исследование вытянутого (ориентированного) волокна.

Как отмечалось выше, изотактический полипропилен в кристаллической области должен образовывать спираль. Полагают, что структурное звено, образующее полимер

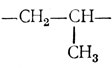
имеет такую геометрию, которая приводит к возникновению кристаллографического периода вдоль полимерной цепи. Это может выполняться путем проведения соответствующих поворотов и переносов химических связей вдоль оси спирали (рис. 10.20). На основании соображений о геометрии молекулы исследователи пришли к выводу, что молекула должна иметь структуру, в которой боковые метильные группы расположены как можно дальше друг от друга. Необходимость такого расположения приводит к образованию спирали, в которой угол между метальными группами составляет 120°, если смотреть вдоль оси спирали (рис. 10.20). Шаг спирали соответствует трем мономерным звеньям.

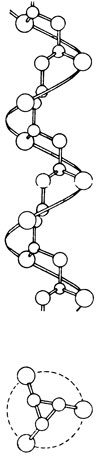
Рис. 10.20. Спиральная структура изотактического полипропилена. На схеме, изображающей вид молекулы сверху (вдоль оси спирали), видно, что метильные группы отстоят друг от друга на максимальное расстояние - 120°

Рентгенограмма волокна из полипропилена имеет отчетливый рефлекс на меридиане при 0,154 Å^-1, что соответствует периоду 6,5 Å. Это расстояние полностью согласуется с полученной ранее моделью спирали, содержащей в одном витке три мономерных звена.

Затем были рассчитаны размеры элементарной ячейки. Их значения можно определить из рентгенограммы. Рефлекс, наблюдаемый на меридиане при 6,5 Å, дает размер элементарной ячейки по оси цепи, а рефлексы, наблюдаемые вблизи экватора, позволяют определить два других размера. Из рентгенограммы можно определить значения углов, образуемых сторонами элементарной ячейки. В табл. 1 приведены результаты, полученные для полипропилена.

Таблица 10.1. Параметры элементарной ячейки полипропилена

Поскольку два угла составляют 90°, элементарная ячейка принадлежит к классу моноклинных кристаллов^*. На основании этих размеров можно рассчитать объем элементарной ячейки; по ним определяют также плотность (d′) одного мономерного звена:

^* (Существует семь классов кристаллов: кубический, моноклинный, триклинный, ромбический, тригональный, тетрагональный и гексагональный.)

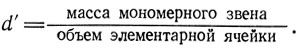
Тщательными измерениями были получены экспериментальные значения плотности. Для полипропилена

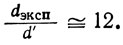
Следовательно, для полипропилена в элементарную ячейку входит 12 мономерных звеньев, что было использовано для вычисления идеальной кристаллографической плотности (d_крист) (рис. 10.21): d_крист= 12×d′=0,9379 г·см^-3 (для изотактического полипропилена).

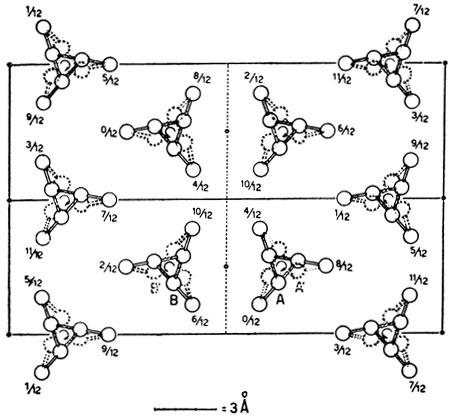
Рис. 10.21. Модель упаковки цепей полипропилена в элементарной ячейке. Как можно видеть, при рассмотрении структуры сверху, вдоль оси, элементарная ячейка содержит равное число правых и левых спиралей. Цифры, приведенные на рисунке, изображают относительные высоты (координата z) атомов в элементарной ячейке

Затем Натта и Коррадини определили тип упаковки изотактического полипропилена для того, чтобы отнести его решетку к одной из 230 возможных пространственных групп. Пространственная группа симметрии определяется типом и числом элементов симметрии кристаллической решетки. Центры симметрии, плоскости симметрии, поворотные оси и плоскости отражения входят в число рассматриваемых операций симметрии. Знание пространственной группы, к которой относится полипропилен, позволяет исследователю на основании рентгенограммы судить о параметрах упаковки и создать модель, показывающую, как спиральная цепь изотактического полипропилена упакована в кристаллической области.