
Все течет, все изменяется
Заботы натуралиста-коллекционера, или как законсервировать динамическую структуру. Гераклитово "Все течет..." и динамическое равновесие живой природы. Динамические структуры на всех уровнях биологической организации. Можно ли рассчитать динамические структуры? ЭВМ управляет процессами технической микробиологии, рассчитывает дозировку лекарств, следит за работой внутренних органов и биологическим равновесием в жидкостях, содержащихся в нашем теле.
В начале книги мы сравнивали былинку и телевизионную башню, сравнивали формы биологического и технического объектов. Затем мы заинтересовались внешним видом живых организмов и установили, что форма растений и животных тесно связана с их функциями и возможностями. Мы обнаружили, что с помощью чисел и математических формул можно описать внешний вид биологического объекта и его изменение, можно судить о сходстве и различии форм. Как выяснилось уже в первой главе, глубокое понимание формы живых организмов немыслимо без знания различных жизненно важных процессов. Теперь пойдем дальше и постараемся объяснить особенности формы организма, исходя из его функции.
Конечно, зависимость между формой и образом действия, иными словами, между структурой и функцией, характерна и для неживой природы. Часы будут казаться нам бессмысленным предметом из латуни и стали до тех пор, пока мы не поймем, как сцепляются шестеренки, как заводная пружина приводит в действие весь механизм и для чего, собственно говоря, движутся стрелки на циферблате. Если мы определим эту связь, то сможем понять, почему шестеренок именно столько, а не больше или меньше, почему эта шестеренка именно такого размера, а та - другого и т. д. Аналогичным образом в первой главе мы пытались понять связь между структурой и функцией в биологических системах: почему кости имеют определенную толщину, почему мышь не может быть меньше и прочее. Это одна сторона структурно-функциональной связи, принцип которой в равной мере справедлив как для технических, так и для биологических объектов. Если глубже вникнуть в проблему формы живых организмов, то откроется другая сторона, которая имеет решающее значение.
Предположим, мы приобрели исключительно дорогие наручные часы. Это украшение, образец элегантности и точности, символ респектабельности, вещь далеко не повседневная. Мы храним часы в чистом сухом месте с возможно меньшими колебаниями температуры. Мы надеваем их лишь в особых случаях, а затем снова упаковываем. При таком обращении часы сохранят свою работоспособность исключительно долго. Зубчатые колесики не сотрутся, а рубины будут казаться новыми даже нашим далеким потомкам.
Теперь обратимся к биологии. Допустим, коллекционер, поймав редкого жука, бабочку или найдя ценное растение, хотел бы присоединить находку к своей коллекции или передать музею. При этом желательно, чтобы образец как можно больше походил на живой, а по возможности даже был таковым. К сожалению, это исключено. Даже при хорошем уходе животное живет лишь ограниченное время, и нам не удастся сколько-нибудь значительно увеличить время жизни растения, если мы срежем его и поставим в воду. Основная причина наших неудач заключается в том, что структура организма связана с его функцией. Вне функции она мертва. Когда "часовой механизм" живого организма не работает, его "шестеренки" ломаются.
Следует отметить, что современные методы позволяют замораживать и длительное время сохранять жизнеспособные клетки и части органов. Сперма может долго находиться в жидком азоте при температуре -196° С, а после оттаивания снова оказывается способной к оплодотворению. Поговаривают уже о "банке органов", где в замороженном виде будут храниться "запасные части" человеческого тела. Правда, пока еще ни разу не удавалось восстановить жизнедеятельность какого-либо высшего организма после замораживания, но с развитием науки и эта проблема, по-видимому, будет решена. И не исключено, что когда-нибудь мы увидим в жидком гелии Спящую Красавицу.
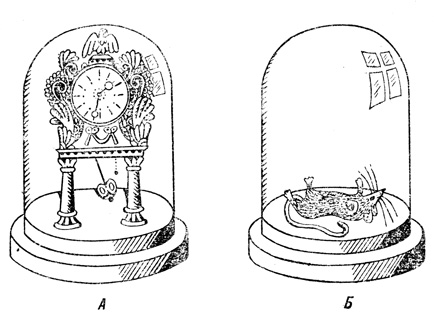
В технике статические структуры (А) хорошо сохраняются, если их герметически изолировать от внешних воздействий, таких, как влажность воздуха, колебания температуры, свет и т. д. Динамические биологические структуры (Б) связаны с окружающей средой обменом веществ. Изоляция приводит их к гибели
Этот факт ни в коей мере не противоречит нашему постулату о связи между структурой и функцией. Позже мы еще вернемся к разговору о теплоте и температуре. При очень низкой температуре все процессы жизнедеятельности приостанавливаются, в том числе и процессы разложения биологических структур. В отличие от этого механизм часов сохраняется при температуре, которая может быть намного выше или ниже температуры, необходимой для их нормальной заботы.
Принцип сохранения структуры через ее функцию заложен в самом устройстве биологической системы. Почти во всех видах клеток действует механизм, который обеспечивает непрерывную замену старых разрушающихся молекул новыми. И лишь немногие клетки, как, например, уже упоминавшиеся красные кровяные тельца, способны только "изнашиваться". Итак, подведем итоги. Биологические структуры отличаются от технических тем, что при функционировании системы они не изнашиваются, а, наоборот, непрерывно восстанавливаются и поддерживаются, другими словами, функционирование системы является для них условием существования. Как говорил Томас Манн, жизнь колеблется между "ограничивающими ее процессами распада и обновления". Об изменчивости жизни, живых структур люди задумывались еще давно. Древнегреческий философ Гераклит (500 г. до н. э) написал свое знаменитое rcavta pel: "Все течет, все движется и ничто не остается неизменным". Два века спустя эту же мысль высказывал Аристотель.
Мы, как современные естествоиспытатели, будем пользоваться современным языком. Так, в случае шестеренки, неживого, технического изделия, мы говорим о статической структуре, тогда как живую, биологическую систему, например клетку, мы называем динамической структурой. Структура - это нечто видимое и относительно постоянное. Для статической структуры такие свойства очевидны. Шестеренка изготавливается и в процессе работы медленно изнашивается. Ее форма, масса "стационарны", т. е. постоянны, независимы от времени (естественно, в определенных границах).. Что же происходит с динамической структурой? Поскольку эта структура непрерывно разрушается и вновь восстанавливается, ее постоянство заключается только в том, что процессы распада и обновления точно компенсируют друг друга и любое влияние на эти процессы приводит к изменению структуры.
Вспомним надувные резиновые фигуры, на которых с таким удовольствием летом плавают дети.
Если такая игрушка цела и невредима, то достаточно надуть ее один раз, чтобы образовалась статическая структура, форма которой не изменяется в течение некоторого времени. Совсем иное дело, если в ней где-нибудь появится дырка, пропускающая воздух. Обычно в таком случае мы либо заклеиваем дырку либо выбрасываем испорченную игрушку. Но ее можно было бы использовать в качестве модели динамической структуры. Непрерывно подкачивая в игрушку воздух, мы тем самым компенсируем утечку, и резиновый зверь остается более или менее плотным. Выходящий из дырки воздух все время заменяется новым. Утечка воздуха через дырку не постоянна, а зависит от давления. Если надувать игрушку более интенсивно, давление внутри нее повысится и утечка воздуха усилится. Для каждой скорости надувания устанавливается в соответствии с внутренним давлением своя скорость утечки.
Итак, мы видим, что в отличие от статических, динамические структуры регулируются процессами, обусловливающими их разрушение и восстановление. Это очень важная мысль, она объясняет, почему биологические объекты приспосабливаются к изменяющимся условиям много лучше, чем любые технические системы.
Состояние, при котором распад уравновешивается синтезом, называют динамическим равновесием. Этот термин полвека назад предложил Людвиг фон Берталанфи. С тех пор теория динамического равновесия приобрела в биологии большое значение.
Весьма наглядную модель динамического равновесия представляет сосуд со стоком. Если в такой сосуд наливать сверху воду, она будет вытекать снизу. Вначале приток больше, чем сток, и уровень воды постепенно повышается. Но с повышением уровня растет давление, а следовательно, увеличивается скорость вытекания воды. В какой-то момент приток и сток уравновесят друг друга и в сосуде установится некий постоянный уровень воды, т. е. будет достигнуто не зависимое от времени состояние динамического равновесия. Оно поддерживается, конечно, до тех пор, пока приток воды остается неизменным. Если скорость притока увеличить, уровень воды вновь начнет подниматься, пока не установится новое равновесное состояние. И наоборот, если приток воды уменьшить, ее уровень понизится. Аналогичным образом система реагирует и на изменение стока.
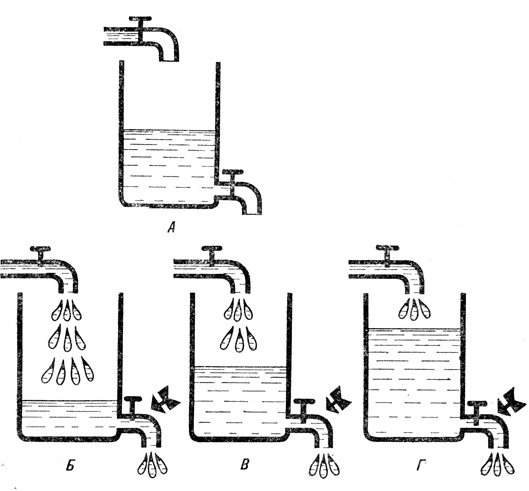
Наполненный водой резервуар с притоком и стоком является хорошей моделью для описания стационарных, т. е. не зависимых от времени, состояний системы. А - статическая структура (оба крана закрыты), которая постоянна из-за отсутствия процессов, зависящих от энергии; Б, В, Г - динамические структуры в различных состояниях равновесиях, которые зависят от положения сливного крана
Однако оставим нашу модель. Она достаточно наглядна, и возникающие в ней изменения можно легко наблюдать. А встречается ли в живой природе состояние динамического равновесия? Оказывается, это основной принцип функционирования живой системы, который реализуется на всех! уровнях биологической организации.
Начнем с молекул. В последние годы стало возможным получать радиоактивные изотопы всех элементов, в том числе и многих биологически важных. Существуют изотопы, которые химически и биохимически ничем не отличаются от "нормальных" атомов, но их присутствие легко обнаружить по регистрируемому приборами излучению. При помощи этих так называемых радиоактивных изотопов можно "метить" молекулы и следить за индивидуальной заменой одной молекулы другой, а также наблюдать и измерять восстановление отдельных частей молекулы. Эксперименты показали, что все молекулы более или менее быстро заменяются новыми и что постоянство биохимического состава есть не что иное, как состояние динамического равновесия, которое поддерживается на протяжении всего времени существования организма.
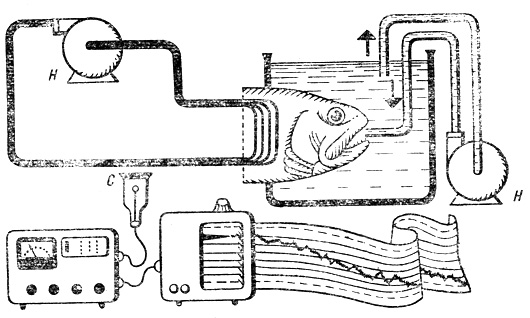
Радиоактивные изотопы позволяют изучать системы, находящиеся в состоянии динамического равновесия, и определять их параметры. В данном случае с помощью изотопа Са45 измеряется кальциевый обмен в крови рыбы. Под действием двух насосов Н раствор циркулирует, в двух замкнутых системах - во внешней среде и кровеносной системе рыбы. Счетчик С регистрирует радиоактивность

Динамическое равновесие на различных уровнях биологической организации. А - молекулярный; Б - субклеточный (митохондрии); В - клеточный; Г - органы и организмы; Д - биоценоз
Поскольку состав молекул непрерывно обновляется, то построенные из них клеточные компоненты - митохондрии, хлоропласты, ядро, наружная клеточная мембрана и т. д. - представляют собой не статические элементы, которые можно сравнивать с техническими изделиями, а динамические структуры, распадающиеся и синтезируемые при динамическом равновесии. Динамика заметна и в ионном составе содержимого клетки. В клетке поддерживается ионная среда, по своему составу совершенно отличная от окружающей, хотя в большинстве случаев суммарная концентрация ионов в клетке такая же, как и во внешней среде. По отношению к окружающей среде клетка "изотонична"*, ибо в противном случае высокие давления, вызванные процессами осмоса, разрывали бы клетку, тем не менее ионный состав ее иной. Например, в сыворотке крови человека ионов натрия содержится примерно в 10 раз больше, чем ионов калия, а внутри эритроцита соотношение концентраций этих ионов совершенно обратное. В результате возникают сильные градиенты концентраций, благодаря которым ионы калия выходят из клетки, а ионы натрия стремятся внутрь нее. Клетка подобна кораблю, давшему течь, и, чтобы предотвратить гибель этого "корабля", постоянно работают ионные "насосы", удаляя натрий и "накачивая" калий.
* (Изотоническими называются растворы, имеющие одинаковое осмотическое давление. В данном случае имеется в виду, что внутри клетки осмотическое давление такое же, как во внешней среде. - Прим. рeд.)
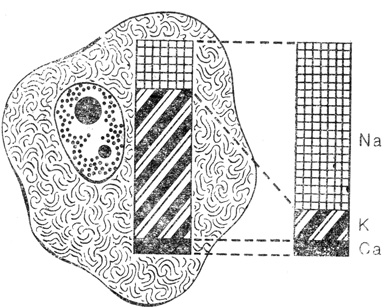
Хотя суммарная концентрация ионов в клетке такая же, как и во внешней среде, концентрации отдельных ионов, особенно ионов калия (К) и натрия (Na), существенно отличаются. Такие жизненно важные для клетки различия поддерживаются специальными ионными насосами, локализованными в клеточной стенке. Однако под действием разности концентраций ионы непрерывно стремятся назад и в результате возникает динамическое равновесие, подобное тому, которое устанавливается в резервуаре с водой
Таким образом, концентрация ионов в клетке поддерживается на достаточно постоянном уровне и находится в динамическом равновесии. Аналогичным образом ведут себя и другие вещества, содержащиеся внутри клетки. Динамическое равновесие другого рода присуще различным органическим молекулам, которые разлагаются в клетке в процессе обмена веществ. Их называют метаболитами. Такие соединения, как, например, разного рода сахара, пассивно проникают (диффундируют) или засасываются клеткой и подвергаются здесь разложению. Следовательно, это не приток и сток, которые взаимно компенсируются, а приток и уничтожение. Такие процессы весьма многочисленны.
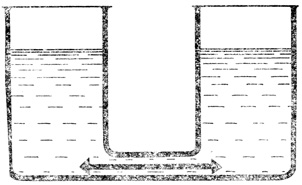
В сообщающихся сосудах обмен водой продолжается и после того, как уровни в них установились. В этом легко убедиться, подкрасив воду в одном из сосудов. Тем не менее такая структура является статической, ибо процесс обмена здесь не требует затрат энергии
Далее мы еще будем говорить об энергетическом балансе таких процессов. Здесь же мы только отметим, что не все системы, в которых происходит обмен, относятся к системам динамического равновесия. Представим себе два сообщающихся сосуда. Когда уровни воды в них выравниваются, обмен воды все равно продолжается за счет самодиффузии; но, поскольку этот процесс не связан с преобразованием энергии, подобная система является статической, а не динамической.
Хотя живая клетка как строительный кирпичик животного или растения в целом является динамической структурой, находящейся в состоянии динамического равновесия, некоторые из ее частей имеют статическую природу. Во многих случаях содержание воды в клетке пассивно регулируется ее энергетическим уровнем. В этом отношении клетку можно смело сравнивать с сообщающимися сосудами. Правда, энергетический уровень клетки определяется не силой тяжести, а сложным взаимодействием различного вида энергий. Однако об этом несколько позже.
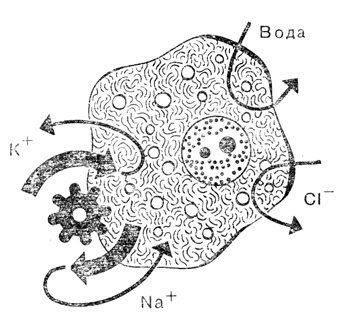
В клетке ионы калия (К+) и натрия (Na+) активно 'перекачиваются' (шестеренка и жирные стрелки) и пассивно возвращаются назад (тонкие стрелки), в то же время обмен водой и ионами хлора (Сl-) происходит только пассивно, подобно тому как это осуществляется в сообщающихся сосудах
Вначале, обсуждая возможности консервации технических и биологических систем, мы говорили о различии между статическими и динамическими структурами. Теперь же необходимо отметить, что многие компоненты клетки, а следовательно, и всего организма являются структурами статическими. Заглянем в биологический музей. Мы найдем там животных и растения, которые хорошо сохранили свою форму, а частично и окраску. Засушенное растение легко сохраняется десятилетиями, так же как засушенный жук, рак, бабочка, морская звезда или рыба. Отсюда следует, что некоторые части живого организма, в основном те, от которых зависит его форма, т. е. элементы скелета, представляют собой статические структуры, хотя и являются продуктами динамических структур. В определенной степени организм обладает возможностью при необходимости, например в случае повреждений, приводить статические структуры в активное состояние, обеспечивая тем самым их изменение и восстановление.
Мы несколько отклонились от темы, коснувшись проблемы динамического равновесия на клеточном уровне. Теперь мы знаем, что организм в целом представляет собой динамическую структуру, хотя отдельные его части могут иметь статическую природу. Но вернемся к нашей основной темe и попытаемся найти другие, более высокие структурные уровни биологической организации.
Следующую ступень в этой организации составляют биологические системы, образованные совокупностью клеток. К ним можно отнести ткани, органы и целые организмы. Клетки нашего тела постоянно отмирают и заменяются новыми. Исключение составляет только нервная система. Очевидно, специализация нервных клеток слишком высока, чтобы их можно было заменить. Установлено, что из имевшихся вначале 10 млрд. нервных клеток 10 тыс. ежедневно безвозвратно теряются. До сих пор остается загадкой, как наш мозг безболезненно переживает такую потерю.
Клетки других систем восстанавливаются. Типичным примером может служить кровь. Продолжительность жизни эритроцитов у человека в среднем равна 100-120 дням, примерно столько же живут и другие клеточные компоненты крови. Кровь с точки зрения ее состава можно рассматривать как динамическую систему. Если врач установит болезненные изменения в составе крови пациента, то причина их может скрываться как в кроветворении, так и в управляемом процессе разрушения кровяных клеток.
Естественно, что у большинства читателей понятие "управляемый" ассоциируется с кибернетикой. И в самом деле, здесь речь идет в какой-то мере о кибернетической проблеме. О кибернетике, в том числе биологической, написано очень много, поэтому обсуждать этот вопрос мы не будем. Позже мы слегка коснемся кибернетической стороны вопроса,
Заметим, что развитие раковой опухоли можно рассматривать как нарушение динамического равновесия. Внезапно возникающее бурное размножение клеток при прежней скорости их разрушения вызывает увеличение количества клеток подобно тому, как повышается уровень воды в описанном выше резервуаре. Об этом мы также поговорим в дальнейшем.
Пример с клетками крови уже предопределяет переход к биологическим системам следующего, более высокого уровня - биоценозу. Биоценоз - это сообщество одинаковых или различных живых организмов. Деревенский пруд с его водными растениями, водорослями, одноклеточными, червями, дафниями, личинками насекомых и рыбами представляет собой биоценоз; то же можно сказать о луге с его растениями, животными; лесе, болоте и т. д. На горьком опыте человек узнал, что такие экосистемы (биоценозы) являются едиными сложными структурами, узнал после того, как жестоко поплатился за вырубку лесов и истребление некоторых видов животных.
Поскольку мы достаточно говорили о сущности динамического равновесия, теперь нам нетрудно обнаружить динамику в миграции животных, их размножении и гибели. Примечателен тот факт, что в природе взаимосвязь животных и растений, хищника и жертвы играет большую роль. На этом уровне взаимодействие между отдельными элементами системы становится особенно заметным. Очевидно, что в системе, все без исключения элементы которой состоят из отдельных живых объектов, каждая структура должна иметь динамическую природу. Статические структуры, которые мы наблюдаем как на клеточном уровне, так и на уровне отдельных организмов, здесь просто немыслимы. Но, конечно, статические структуры оказывают определенное влияние на динамическое равновесие в живой природе. Правда, эти структуры - характеристика почвы, температура, глубина (для водных биоценозов) и т. д. - представляют собой компоненты неживой природы.
У читателя, возможно, сложилось мнение, что эта глава в отличие от предыдущих не имеет ничего общего с физикой и математикой. Действительно, до сих пор мы довольствовались лишь общими рассуждениями о сущности динамического равновесия. Мы узнали, что биологические системы находятся в состоянии динамического равновесия, т. е. одновременно в статическом и динамическом состояниях. Динамическое равновесие обеспечивает, например, регулярное сокращение клеток сердечной мышцы, готовность к возбуждению у нервных клеток, выделение секрета клетками желез. Динамическое равновесие определяет нормальный качественный и количественный состав клеток крови, "цветение" водорослей в пруду, количество микроорганизмов в промышленных установках по непрерывному производству спирта, пенициллина и т. д.
Из этих примеров видно, как важно знать и заранее рассчитывать условия возникновения динамического равновесия и критерии его устойчивости. Анализ динамического равновесия с помощью "маркированных"* компонентов требует хорошего знания математики и физики. Такие задачи решают сейчас с помощью сложных электронных вычислительных машин. Однако мы попытаемся рассмотреть некоторые принципы теории динамических систем, не углубляясь особенно в математику.
* (Отдельные компоненты динамических систем можно маркировать, т. е. метить, по-разному. Например, при анализе молекулярных систем используют радиоактивные изотопы, при анализе популяций микроорганизмов - генетические метки и т. д. - Прим. ред.)
Динамическое равновесие, как мы установили, есть такое изменяющееся состояние, при котором уравновешиваются приток и сток, размножение и гибель, синтез и разрушение. Поэтому условие динамического равновесия мы можем записать в виде простого уравнения
JAB = JBA.
Величину J в биофизике называют потоком. С помощью этой величины выражают скорости притока и стока, синтеза и разрушения, частоту размножения и гибели. Иногда это может быть направленная величина, или, как говорят математики, "вектор", иногда просто число - "скаляр". Но в любом случае данный параметр связан со временем: приток в единицу времени, размножение в единицу времени, распад в единицу времени и т. д. Буквы АВ и ВА (индексы при символах потоков) характеризуют направление потока: АВ означает "от А к В", а ВА - "от В к А", т. е. потоки JАВ и JВА противоположны друг другу. В большинстве случаев состояние динамического равновесия определяется не одним, а несколькими потоками, и величины JАВ и JВА представляют тогда сумму потоков в соответствующем направлении.
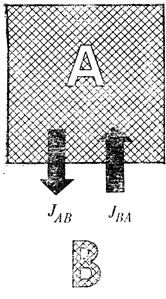
Схематическое изображение системы, находящейся в состоянии динамического равновесия. JAB - приток; JBA - cток
Итак, наш разговор уже перекинулся в область биофизики. От общих рассуждений мы перешли теперь к конкретным величинам. Как рассчитывать потоки? Поток - это движение, а каждое движение должно быть обусловлено какой-то силой. Вначале мы просто предполагаем ее наличие и интересуемся возникающими при этом потоками, не задумываясь о происхождении самой силы. Последнее относится к области биоэнергетики, или термодинамики, - науки о преобразовании энергии. Но о ней мы поговорим в следующей главе.
Пусть задана некая "обобщенная" сила: механическая, электрическая или "биологическая". Она является причиной движения, и эту причинную связь мы хотели бы выяснить.
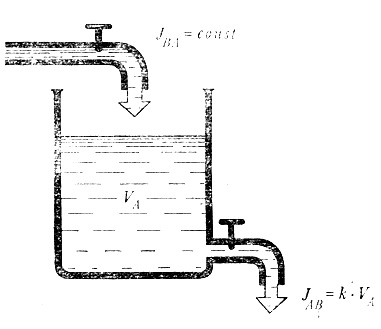
Динамическое равновесие легче всего рассчитать для резервуара с водой
Проще всего это сделать на примере резервуара с водой. Предположим, приток воды в нем постоянен и зависит только от того, насколько открыт кран. Значительно сложнее обстоит дело со стоком. Даже в том случае, когда на протяжении всего опыта положение крана остается без изменений, скорость вытекания воды через сливную трубу изменяется пропорционально гидростатическому давлению в сосуде. При увеличении давления вдвое через отверстие вытекает вдвое больше воды. Если сосуд цилиндрический, давление прямо пропорционально объему воды. Действительно, в этом случае удвоение объема воды приводит к удвоению высоты водяного столба и, следовательно, к удвоению давления. Мы можем записать
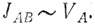
Сток, т. е. поток от А к В, пропорционален объему воды в резервуаре. Знак пропорциональности можно заменить знаком равенства, если ввести некую константу потока, или, как ее иначе называют, константу обмена. Она имеет размерность 1/время (например, 1/мин), а произведение ее на объем дает поток, в данном случае - скорость течения (объем/время). Итак, мы имеем
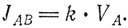
Это линейное уравнение потока. Линейным оно называется потому, что переменная величина VA входит в уравнение в первой степени, а не в квадрате и не в произведении нескольких переменных. Так как объем VA зависит от времени, т. е. является функцией времени, обозначим объем, занимаемый водой при наступлении равновесия, через VAРАВН. Как мы уже отмечали, при равновесии JАВ = JВА, следовательно,
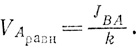
Этот простой расчет помог нам выявить важный закон поведения линейной системы - закон "стремления к одному и тому же конечному состоянию".
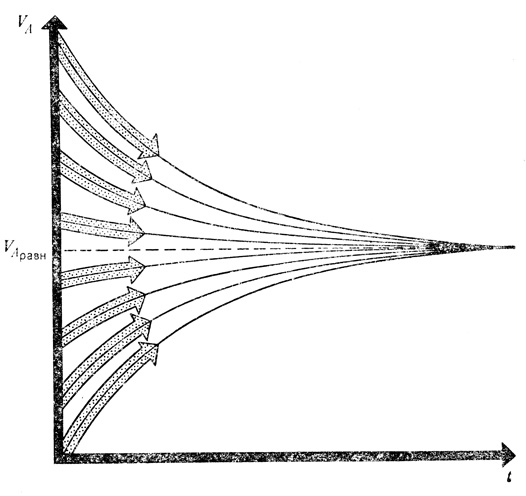
Система независимо от ее начального состояния стремится в своем развитии к одному и тому же конечному состоянию. В рассматриваемом случае это равновесный объем VАравн, который определяется только скоростью обмена. Множество кривых, вы-ходящих из разных начальных точек, стремится к этой величине
Объем воды в резервуаре VA полностью определяется скоростью притока JВА и константой стока k и совершенно не зависит от того, какое количество воды было в резервуаре в начальный момент времени. Мы можем легко убедиться в этом экспериментально. Подставим сосуд с отверстием под равномерно текущую струю воды. Довольно быстро в сосуде установится динамическое равновесие. Отметим чертой уровень воды и, не убирая сосуда из-под струи, быстро нальем в него воду из другого сосуда. Уровень воды резко поднимется, но не останется таким, а постепенно опустится до отмеченного чертой положения. То же произойдет, если мы искусственно понизим уровень воды. Стремление к одному и тому же конечному состоянию означает, что система рано или поздно вновь приходит к нему независимо от своего исходного состояния. Эта ситуация наглядно представлена на рисунке.
Данный закон применим и к биологической системе. Многие из рассмотренных нами биологических систем, находящихся в состоянии динамического равновесия, при кратковременном воздействии извне вновь возвращаются к своему постоянному положению, определяемому параметрами системы. Позже мы увидим, что нелинейные системы не подчиняются действию этого закона.
Вернемся к соотношению потоков. До сих пор мы рассчитывали, только конечное состояние системы VAРАВН. Из рисунка видно, что величина VA может по-разному изменяться во времени. Попытаемся обосновать это теоретически.
Закроем кран, из которого вода поступает в резервуар. Уровень воды в сосуде понизится. Скорость понижения уровня определяется отношением изменения объема к интервалу времени. Сначала уровень воды понижается быстро, потом медленнее. Полученное отношение, таким образом, непрерывно изменяется, и поэтому лучше рассматривать "бесконечно малое" изменение объема в "бесконечно малый" интервал времени. "Бесконечно малое" отличие одной величины от другой дает "бесконечно малую" разницу, или "бесконечно малое" приращение, которое математики называют дифференциалом и обозначают символом d. Следовательно, dVA есть дифференциал объема и обозначает как раз "бесконечно малое" изменение объема. Соответственно dt - это бесконечно малый интервал времени. Составив отношение dVA/dt (математики говорят не "dVA на dt, a dVA no dt"), мы получим известное каждому старшекласснику отношение дифференциалов, или производную.
Если вода из сосуда не испаряется, то ее объем уменьшается лишь за счет стока. Тогда мы можем записать
| - | d VA | = JAB |
| dt |
Знак "минус" означает, что положительный сток вызывает отрицательное изменение объема, т. е. его уменьшение. С учетом уравнения потока получим
| - | dVA | = k ⋅ VA |
| dt |
Это очень важное уравнение, которое справедливо для многих процессов, происходящих как в живой, так и в неживой природе. Оно показывает, что скорость изменения величины, определяемая производной dVA/dt, прямо пропорциональна самой величине - в данном случае VА. Чем больше VA, Т. е. чем дальше кривая удалена от оси абсцисс, тем круче она снижается.
Это уравнение справедливо для случая, когда верхний кран в резервуаре закрыт. Если мы откроем его и обеспечим постоянный приток воды в единицу времени JВА, то изменение величины VА будет определяться другим уравнением:
| dVA | = - kVA + JBA. | |
| dt |
Это уже общее уравнение, которое описывает изменение уровня воды в зависимости от времени в сосуде с двумя открытыми кранами.
Когда система достигает динамического равновесия, VA больше не изменяется, следовательно, dVA/dt = 0, а величина VA в уравнении становится равной V Aравн. Тогда
0 = - kVAравн + JBA.
Как легко заметить, здесь обнаруживается та же связь между объемом VAРАВН и потоком JВА, о которой мы говорили выше.
Однако вернемся к общему уравнению динамической системы. Так как переменная VА входит в него не только непосредственно, но и через отношение дифференциалов dVA/dt, такое уравнение называется дифференциальным. Дифференциальные уравнения составляют весьма солидный раздел математики, но здесь мы, разумеется, не имеем возможности его рассматривать. Обсудим только некоторые особенности уравнений такого рода. Решить уравнение - значит найти число, которое, будучи подставленным в уравнение, превращает его в тождество. В отличие от обычных алгебраических уравнений дифференциальное уравнение имеет своим решением не число, а функцию. Поэтому часто говорят не о решении такого уравнения, а о его "интегрировании". Интегрирование есть операция, в известной степени обратная дифференцированию. Поэтому в данном случае интегрирование означает такое преобразование уравнения, при котором производная исчезает.
Учащиеся обычно недолюбливают операцию интегрирования. В то время как производные можно получить, зная общие правила дифференцирования, для интегрирования необходимо знать правильный "прием". И хотя во многих конкретных случаях существуют определенные правила нахождения решения, сформулировать ход решения в общем виде нельзя. Иногда интегрирование вообще невозможно. Поэтому не всякое дифференциальное уравнение можно решить аналитически, иногда приходится довольствоваться приближенными машинными расчетами.
Каждый, кто знаком с основами интегрального исчисления, знает, что в решение интеграла обязательно входят постоянные интегрирования. Необходимость в них отпадает только для так называемых определенных интегралов, в которых пределы изменения функции четко очерчены. Постоянные вводятся и при решении дифференциальных уравнений. Сначала интегрирование дает нам общее решение: бесконечное множество кривых определенного вида. И только после того, как мы находим начальные условия, мы можем "выудить" из них "частное решение".
Это хорошо видно из рисунка, показывающего изменение объема воды в резервуаре. Представленные на нем кривые являются различными частными решениями, которые относятся к разным начальным условиям, но в итоге все кривые стремятся к одному и тому же значению VAравн.
Чтобы сделать наше довольно сухое и, казалось бы, столь далекое от биологии изложение более понятным, оглянемся на пройденный путь и подведем некоторые итоги.
Сначала мы установили, что динамическую систему, например обмен веществ в клетке, можно сравнить с резервуаром, в который вода поступает через один кран и вытекает через другой. Затем мы попытались сделать кое-какие расчеты. Для этого мы ввели понятия обобщенной силы и потока, установили соотношения между ними. Оказалось, что в динамической системе изменение величины можно выразить отношением дифференциалов, а поведение всей системы описать дифференциальным уравнением. Решение, или интегрирование, такого уравнения дает нам сначала множество кривых одинакового вида, которые показывают, как будет "развиваться" система из любого исходного положения до тех пор, пока не достигнет стационарного, т. е. не зависимого от времени, состояния динамического равновесия. Особенно важно отметить, что все эти кривые в итоге стремятся к одной точке. Такое поведение простых линейных систем мы назвали "стремлением к одному конечному состоянию". Это свойство и определяет устойчивость биологических систем.
Что же дают нам теоретические представления? Прежде всего они позволяют построить модель любой сложной системы. На рисунке показано, как чисто схематически при помощи гидравлической модели можно представить обмен веществ, протекающий в клетке или в какой-нибудь из ее органелл, например в митохондрии. Если для каждой ячейки (т. е. резервуара) просуммировать потоки по всем направлениям и приравнять их соответствующим отношениям дифференциалов, как мы это делали раньше, то мы снова получим дифференциальные уравнения, решения которых позволяют описать поведение всей системы. Здесь нам опять может пригодиться ЭВМ.
Какое практическое применение имеют подобные расчеты? Допустим, в клинику обращается пациент с заболеванием, причиной которого может быть расстройство функций щитовидной железы. В радиологическом отделении ему дают выпить жидкость, содержащую безвредный для организма быстро распадающийся радиоактивный иод. Счетчик радиоактивности регистрирует интенсивность его излучения в различных частях тела; ЭВМ рассчитывает, исходя из этого, константы скоростей поступления иода в кровь и накопления его в щитовидной железе. На основании этих данных врач может поставить точный диагноз.
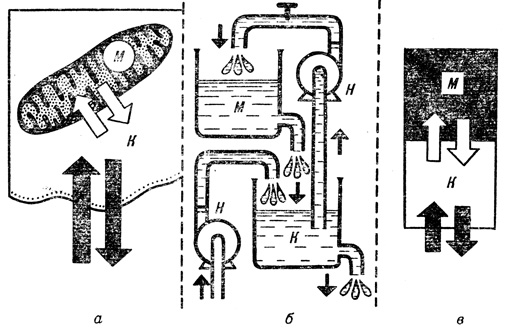
Вещество из внешней среды поступает через клеточную мембрану в клетку К, а затем следует дальше в одну из клеточных структур, 'клеточную органеллу', например митохондрию М (а). Этот процесс можно смоделировать системой из двух наполненных водой резервуаров с насосами Н (б), которые показаны схематически (в). Рисунки расположены в последовательности, соответствующей переходу от конкретной биологической системы к ее все более абстрактному изображению
В медицине довольно часто возникает необходимость в расчетах такого рода. Как применять лекарство, т. е. в каком количестве и через какие интервалы времени следует принимать или вводить данное вещество, чтобы его концентрация в нужном месте была оптимальной? Лекарство попадает в организм и затем разлагается; от частоты его приема зависит уровень равновесной концентрации. А как влияет интенсивность дыхания на снабжение кислородом определенного органа? Как ускорить выведение из организма токсических веществ?
Однако подобные методы позволяют решать не только медицинские задачи. Везде, где биологические процессы имеют народнохозяйственное значение, в сельском, лесном, водном хозяйствах, в пивоваренной промышленности и виноделии, иными словами, там, где микроорганизмы используются в производстве, оптимальные режимы все чаще и чаще рассчитывают именно таким способом.
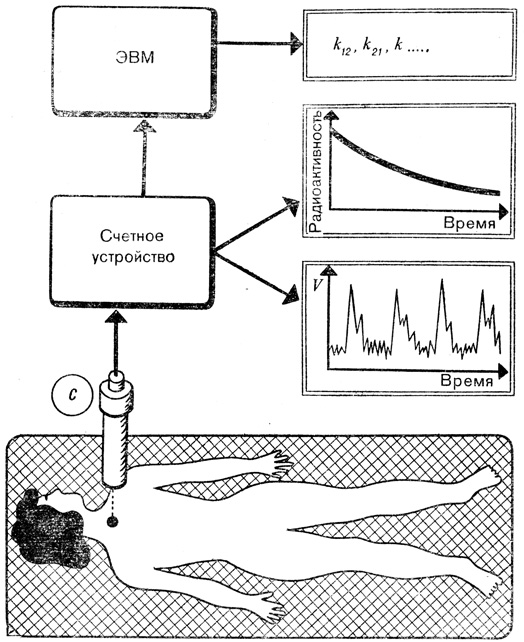
Пример использования системного анализа. Счетчик С регистрирует излучение содержащегося в щитовидной железе радиоактивного иода, который ввели пациенту в целях диагностики. Импульсы регистрируются счетным устройством и записываются в виде кривой изменения радиоактивности во времени. ЭВМ действует по заданной программе и выдает врачу параметры обмена k12, k21..., на основании которых можно поставить точный диагноз
До сих пор мы рассматривали наиболее простые,, так называемые линейные зависимости, где скорость изменения какой-либо величины, т. е. поток, связана с самой величиной постоянным коэффициентом. Но как быть, если этот коэффициент изменяется сам? В этом случае возникают нелинейные зависимости, с которыми мы хотели бы познакомить читателя на примере размножения бактерий. Хотя такие нелинейные зависимости весьма характерны для биохимических реакций и процессов транспорта веществ, иначе говоря процессов, происходящих на молекулярном уровне, процесс размножения бактерий в этом отношении наиболее показателен. А поскольку мы уже упоминали, что динамическое равновесие встречается на всех уровнях биологической организации, то будет также полезно и даже необходимо рассмотреть пример из области экологии.
Нальем в пробирку стерильный питательный раствор, который используют микробиологи для выращивания микроорганизмов, и введем туда небольшое количество бактерий или дрожжей. Допустим, в начальный момент времени в растворе находится 10 клеток, живых и способных к делению. Известно, что каждая из них в определенных условиях через определенный промежуток времени делится. Таким образом, через соответствующий интервал времени в растворе окажется 20 клеток. Спустя еще один такой интервал, их будет 40, потом 80, 160, 320, 640, 1280...
Такой процесс размножения можно описать линейным дифференциальным уравнением. Скорость прироста (назовем ее потоком особей J) в этом случае опять пропорциональна общему количеству (клеток), и, как и в прежнем примере, мы можем выразить ее через отношение дифференциалов. Обозначив количество клеток в пробирке буквой я, можно записать
| dn | = kn | |
| dt |
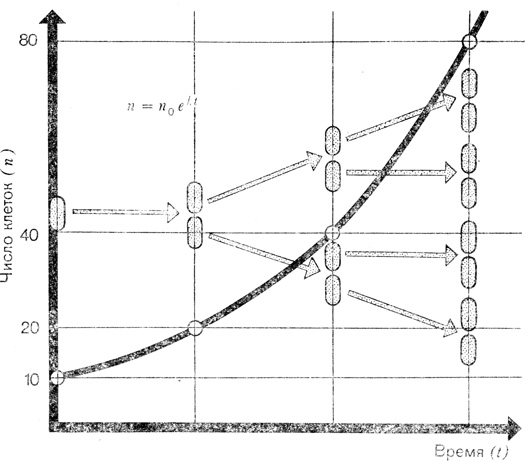
Так выглядит на графике экспоненциальная фаза роста микроорганизмов: из одной клетки получается 2, из 2-4, из 4-8 г. д. При неограниченном запасе питательных веществ такой ост продолжался бы до бесконечности
Это уравнение напоминает уже знакомое нам линейное уравнение потока. И действительно, мы опять получили линейную зависимость, но на сей раз без отрицательного знака. Это означает, что в отличие от предыдущего примера, где количество воды в сосуде течением времени уменьшалось, в данном случае число микроорганизмов увеличивается.
Мы не будем заниматься интегрированием этого равнения. Представленная на рисунке формула есть частное решение его для случая, когда количество бактерий в начале опыта, т. е. в момент времени t = 0, было равно n0. В приведенной формуле появилась новая величина - число е. Это иррациональное число, т. е. число, которое нельзя выразить в виде отношения двух целых чисел; оно равно 2,71828… и является основанием так называемого "натурального" логарифма; им широко пользуются математики. О числе е можно рассказать много интересного, но это уже не имеет никакого отношения к биологии. Вместо е в нашей формуле можно было бы использовать любое другое число, однако в таком случае и величина k стала бы другой.
Как видно, количество клеток n является функцией времени t причем время t в формуле входит в показатель степени. Вообще говоря, прежние наши уравнения также представляют собой экспоненциальные (степенные) функции, в которых k отрицательно, что указывает не на возрастание, а на уменьшение значения функции со временем.
Итак, размножение клеток. Сначала происходящее несколько обескураживает нас. Через каждый промежуток времени концентрация клеток удваивается! К чему же это приведёт в конце концов? Кривая поднимается круче и круче. Это напоминает знаменитую пшенную кашу из сказки о волшебном горшке, которая переполнила дом и вытекла на улицу. Такое может случиться и с маминым тестом и с папиным вином, которое бродит в бутыли. Видимо, наше уравнение в лучшем случае описывает только начало процесса, а затем процесс размножения клеток идет как-то иначе. Что же мы не учли в наших рассуждениях? На самом деле происходит следующее: когда достигается определенная концентрация клеток, питательные вещества среды исчерпываются и бактерии начинают размножаться медленнее, а потом и вовсе прекращают делиться. Как это учесть в уравнении?
Вначале мы приняли, что k - коэффициент пропорциональности, отражающий скорость деления клеток в определенных условиях. Но когда условия ухудшаются, величина k должна уменьшаться. Говоря математическим языком, k теперь уже не постоянная величина, она зависит от числа клеток n. И чтобы идти дальше, нам придется сначала выяснить, какова зависимость k от n. Предположим, что величина k состоит из двух слагаемых. Одно из них пусть будет постоянно; обозначим его k1 и предположим, к примеру, что с ним связаны некие наследственно закрепленные свойства вида, не зависящие от внешних условий. Второе слагаемое отрицательно, и его абсолютная величина возрастает с увеличением числа клеток; обозначим его k2n и будем подразумевать, что за ним кроется какой-либо фактор, сдерживающий развитие, например, борьба за существование или, в нашем случае, борьба за пищу.
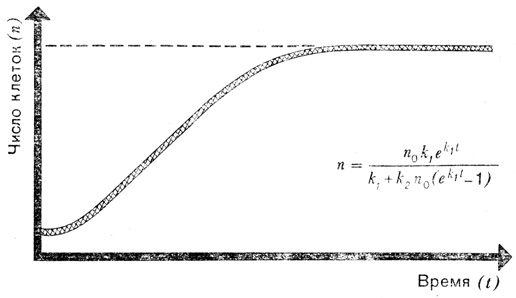
'Логистическая' кривая отражает прекращение размножения клеток после начальной экспоненциальной фазы роста. Уравнение, записанное на рисунке, является наиболее простым из уравнений подобного типа и тем не менее оно намного сложнее приведенного на предыдущем рисунке
Итак,
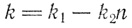
и дифференциальное уравнение принимает вид
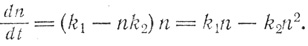
Это уже нелинейное дифференциальное уравнение, в которое входит n2. Чтобы показать, насколько усложняет решение это маленькое дополнение, на рисунке представлено экспоненциальное уравнение, связывающее величины n и t. Но самое важное здесь - новый вид кривой: после быстрого начального подъема кривая стремится к горизонтальной линии, соответствующей равновесному состоянию. Если читатель обладает некоторыми познаниями в алгебре, он может при желании с помощью этого уравнения провести анализ кривой. Легко показать, что при малых значениях t уравнение превращается в простое уравнение экспоненциального роста. При больших же значениях t нелинейные соотношения между скоростью прироста и общей численностью особей (популяцией) приводят к тому, что кривая загибается.
Такое нелинейное поведение популяции растущих, размножающихся организмов или целого биоценоза, живого сообщества, типично для высших уровней биологической организации. Особенно интересные взаимоотношения возникают там, где один вид животных служит кормом для другого. Зависимость "хищник - жертва" около 50 лет назад рассчитал французский ученый Вольтерра, и с тех пор она неоднократно становилась предметом обсуждения.
Представим себе огороженный участок леса, в котором обитают лисы и зайцы. Предположим, что травы там более чем достаточно, так что зайцы не испытывают недостатка в корме, и нам не придется учитывать эту сторону вопроса. Это упростит решение задачи. Зайцы живут и размножаются. У лис тоже есть пища, и они тоже размножаются. Но когда число лис значительно увеличится, они станут истреблять зайцев в большем количестве, и число тех уменьшится. После этого лисы начнут голодать, некоторые из них погибнут, скорость размножения их понизится. Это приведет к вымиранию лис, и в результате уменьшится число истребляемых ими зайцев. Последних опять станет много, у лис снова появится пища, они будут быстро размножаться, уничтожать зайцев и т. д.
Как показывает этот забавный мысленный эксперимент, динамическое равновесие в данном сообществе так и не наступает: в нем происходят лишь периодические колебания. Это можно доказать математически или, что значительно легче, смоделировать и рассчитать на ЭВМ. Не вдаваясь в детали сложных математических выкладок, рассмотрим результаты таких расчетов. Их можно изобразить графически двумя способами. Если представить количество тех и других животных в зависимости от времени, то мы получим синусоидные кривые; если же на график нанести число зайцев в зависимости от численности лис, то получится так называемый годограф. Если много лис и мало зайцев, точка на годографе скользит направо вниз; зайцы размножились - точка передвинулась налево вверх. Так как синусоиды на верхнем рисунке сдвинуты относительно друг друга, точка на годографе описывает замкнутую кривую. Такой график в честь уже упоминавшегося нами ученого назван циклом Вольтерра. Разумеется, цикл Вольтерра никогда не может касаться оси координат, ибо это значило бы, что вид вымер. В таком случае игра пришла бы к естественному концу. В некоторых случаях кривая представляет собой не замкнутый цикл, а спираль. Это значит, что происходит сдвиг соотношения в пользу одного из видов.
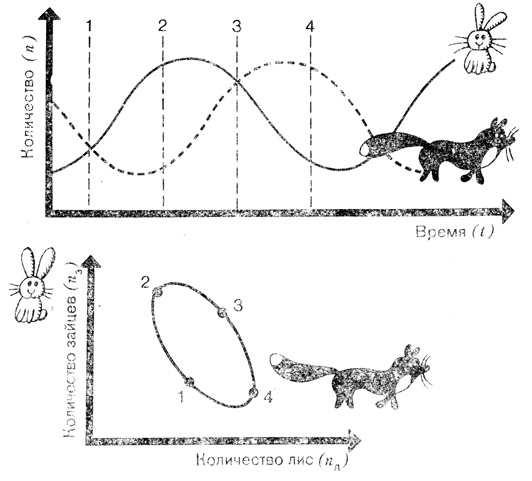
Численность каждого вида в системе хищник - жертва не устанавливается на каком-либо постоянном уровне, а периодически колеблется. Это можно изобразить либо в виде функции n(t), либо в виде годографа n1(n2) (здесь так называемый "цикл Вольтерра"). Отмеченные цифрами точки цикла соответствуют моментам времени, обозначенным на верхнем рисунке
Мы снова приблизились к той границе, где сегодня кончаются наши возможности разумного использования математики в биологии. Расчеты наземных и водных сообществ живых организмов имеют огромное значение для народного хозяйства, но они чрезвычайно сложны. Сейчас такие расчеты пытаются производить только в микробиологии и гидробиологии, где они связаны с проблемами рыбного хозяйства, очистки вод и охраны окружающей среды.
Теоретическое обоснование колебаний, возникающих в экологических системах, появилось лишь после работ Вольтерра, хотя о существовании таких колебаний было известно уже давно. Еще в средние века люди знали, что эпидемии чумы и холеры, против которых они были бессильны, вспыхивают и затухают периодически, волнами. Такие колебания издавна известны и в экологии. Вероятно, большую роль играют здесь сезонные изменения климата.
Чтобы рассчитать подобные явления, происходящие в окружающем нас мире, необходимо осилить чрезвычайно сложные системы уравнений, правильное решение которых далеко не всегда определяется лишь возможностями вычислительной техники. Чем сложнее уравнения, тем большая неопределенность появляется в результатах расчетов, так как даже небольшие изменения каждого из многочисленных коэффициентов приводят к сильной деформации кривой на графике. Для того чтобы произвести оценки, которые могут оказаться полезными для практики, необходимо решить еще множество теоретических вопросов.
Колебательные процессы, которые мы для наглядности рассмотрели на примере из области экологии, можно встретить также на молекулярном и клеточном уровнях. В особенности это касается ферментативных реакций с характерными для них нелинейными зависимостями. Спектр таких экспериментально обнаруженных и теоретически рассчитанных явлений чрезвычайно широк. Так, регулярные отклонения в клеточных процессах, например периодические изменения концентраций, вызывают колебания, сходные с качанием маятника часов. Во многих случаях такие колебания служат индикатором времени для биологических ритмов. Так называемые "биологические часы", т. е. суточные и сезонные колебания биологической активности, несомненно, объясняются теми же явлениями.
Выше мы уже затрагивали проблему устойчивости. Не все динамические системы подчиняются закону, определенному нами как "стремление к одному и тому же конечному состоянию". Некоторые системы не обладают способностью приходить к одному и тому же конечному состоянию из разных исходных точек. От малейшего изменения в начальном состоянии такой системы зависит, каким путем пойдет ее дальнейшее развитие, подобно тому как одна капля дождя, упавшая всего лишь в нескольких метрах от второй, но по ту сторону водораздела, проследует по Дунаю к Черному морю, между тем как другая попадет вместе с водами Эльбы в Северное море.
Заголовок этой главы гласит: "Все течет, все изменяется". Мы рассмотрели здесь биологические системы в их динамике, динамическое равновесие на разных уровнях биологической организации, переходные состояния, колебания. Мы узнали, что под биологическими структурами следует понимать не только клеточные структуры, которые можно наблюдать с помощью оптического или электронного микроскопов, но и распределение концентраций различных веществ или клеток, распределение организмов в популяциях и многое другое. Такие структуры постоянны только благодаря непрерывному процессу распада и синтеза. В этом смысле они менее постоянны, чем статические структуры в технике. С другой стороны, они не так изнашиваются, потому что непрерывно сами себя "ремонтируют". Таким образом, динамика - основа для функционирования живых систем.
Анализируя линейные и нелинейные уравнения, описывающие различные биологические процессы, мы могли оценить степень сложности этих процессов. Говоря, о "стремлении к одному и тому же конечному состоянию" линейных систем и неоднозначности нелинейных, мы тем самым, хотя бы мимоходом, коснулись вопросов развития этих систем.
Читатель, возможно, заметил, что в наших рассуждениях мы совсем не пользовались понятием "кибернетика". Сейчас появилось много книг по биологической кибернетике, так что нам нет необходимости рассматривать здесь это весьма модное научное направление. Но в принципе рассмотренные нами вопросы можно было бы связать с кибернетикой. Известно, что многие биологические процессы управляются посредством обратной связи, и очень трудно определить границу, отделяющую теорию динамического равновесия от кибернетики. Многое из того, о чем мы говорили, можно без всяких оговорок отнести к кибернетике. Во всяком случае, следует знать, что кибернетика это не игра, оперирующая некими более или менее высокими понятиями, как это, к сожалению, часто бывает, а строгая математическая дисциплина, построенная на основе дифференциальных уравнений.
|
ПОИСК:
|
© BIOLOGYLIB.RU, 2001-2020
При копировании ссылка обязательна:
http://biologylib.ru/ 'Библиотека по биологии'
При копировании ссылка обязательна:
http://biologylib.ru/ 'Библиотека по биологии'